Question

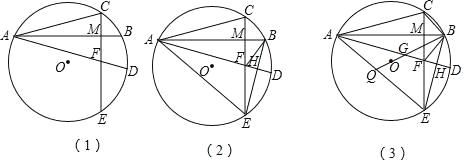
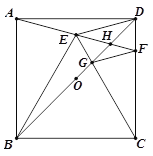
【题目】如图，正方形ABCD中，O为BD中点，以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE、AF于G、H,下列结论：①∠CEH=45;②GF∥DE;③2OH+DH=BD;④BG=DG;⑤.其中正确的结论是（ ）

A. ①②③ B. ①②④ C. ①②⑤ D. ②④⑤

Answer 1

【答案】C

【解析】

解：①由∠ABC=90°，△BEC为等边三角形，△ABE为等腰三角形，∠AEB+∠BEC+∠CEH=180°，可求得∠CEH=45°，此结论正确；

②由△EGD≌△DEF，EF=GD，再由△HDE为等腰三角形，∠DEH=30°，得出△HGF为等腰三角形，∠HFG=30°，可求得GF∥DE，此结论正确；

③由图可知2（OH+HD）=2OD=BD，所以2OH+DH=BD此结论不正确；

④如图，过点G作GM⊥CD垂足为M，GN⊥BC垂足为N，设GM=x，则GN=x，进一步利用勾股定理求得GD=x，BG=x，得出BG=GD，此结论不正确；

⑤由图可知△BCE和△BCG同底不等高，它们的面积比即是两个三角形的高之比，由④可知△BCE的高为（x+x）和△BCG的高为x，因此S△BCE：S△BCG=（x+x）：x=，此结论正确；故正确的结论有①②⑤．故选C．