题目内容
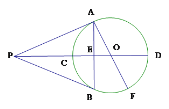
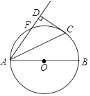
【题目】如图，AB是⊙O的直径，点F、C是⊙O上两点，且 
= 
=
，连接AC、AF，过点C作CD⊥AF，交AF的延长线于点D，垂足为D，若CD=2
，则⊙O的半径为（ ）
A. 2 B. 4 C. 2 D. 4
【答案】D
【解析】
连结BC.由AB为直径得∠ACB=90
,由
= 
=
得∠BOC=60,则∠BAC=30, 新以∠DAC=30, 在Rt△ADC中, 利用含30度的直角三角形三边的关系得AC=2CD=
,在Rt△ACB中,根据勾股定理求得AB,进面求得圆O的半径.
解:连结BC,如图，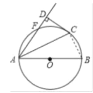
AB为直径，
∠ACB =90.
= =，∠BOC=
=60
∠BAC=30,∠DAC=30.
在RAADC中.CD-2V3.
AC=2CD=.
在Rt△ACB中,
.
即:
AB=8.
圆O的半径为4.
故选D.
【题目】6月14日是“世界献血日”，某市采取自愿报名的方式组织市民义务献血．献血时要对献血者的血型进行检测，检测结果有“A型”、“B型”、“AB型”、“O型”4种类型．在献血者人群中，随机抽取了部分献血者的血型结果进行统计，并根据这个统计结果制作了两幅不完整的图表：
血型 | A | B | AB | O |
人数 |
| 10 | 5 |
|
（1）这次随机抽取的献血者人数为 人，m= ；
（2）补全上表中的数据；
（3）若这次活动中该市有3000人义务献血，请你根据抽样结果回答：
从献血者人群中任抽取一人，其血型是A型的概率是多少？并估计这3000人中大约有多少人是A型血？
（4）现有3个自愿献血者，2人血型为O型，1人血型为A型，若在3人中随机挑1人献血，2年后又从此3人中随机挑1人献血，试求两次所抽血型均为O型的概率．
【题目】一次期中考试中，A、B、C、D、E五位同学的数学、英语成绩有如下信息：
A | B | C | D | E | 平均分 | 方差 | |
数学 | 71 | 72 | 69 | 68 | 70 |
| 2 |
英语 | 88 | 82 | 94 | 85 | 76 | 85 |
|
（1）求这5位同学在本次考试中数学成绩的平均分和英语成绩的方差．
（2）为了比较不同学科考试成绩的好与差，采用标准分是一个合理的选择，从标准分看，标准分大的考试成绩更好，请问A同学在本次考试中，数学与英语哪个学科考得更好？
