题目内容
【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.
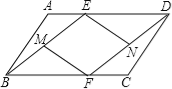
(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
【答案】(1)、证明过程见解析;(2)、平行四边形;证明过程见解析.
【解析】试题分析:(1)根据平行四边形的性质和全等三角形的判定,在△ABE和△CDF中,很容易确定SAS,即证结论;
(2)在已知条件中求证全等三角形,即△ABE≌△CDF,△MBF≌△NDE,得两对边分别对应相等,根据平行四边形的判定,即证.
试题解析:(1)∵ABCD中,AB=CD,∠A=∠C,
又∵AE=CF,
∴△ABE≌△CDF;
(2)四边形MFNE平行四边形.
由(1)知△ABE≌△CDF,
∴BE=DF,∠ABE=∠CDF,
又∵ME=BM=![]() BE,NF=DN=
BE,NF=DN=![]() DF
DF
∴ME=NF=BM=DN,
又∵∠ABC=∠CDA,
∴∠MBF=∠NDE,又∵AD=BC,AE=CF,∴DE=BF,
∴△MBF≌△NDE,
∴MF=NE,
∴四边形MFNE是平行四边形.

练习册系列答案
相关题目
【题目】某汽车专卖店计划购进甲、乙两种新型汽车共140辆,这两种汽车的进价、售价如下表:
进价(万元/辆) | 售价(万元/辆) | |
甲 | 5 | 8 |
乙 | 9 | 13 |
(1)若该汽车专卖店投入1000万元资金进货,则购进甲乙两种新型汽车各多少辆?
(2)若该汽车专卖店准备乙种型号汽车的进货量不超过甲种型号汽车的进货量的3倍,应怎样安排进货方案,才能使该汽车专卖店售完这两种新型汽车后获得的利润最大?最大利润是多少?(其它成本不计)