Question

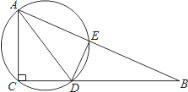
【题目】如图，在四边形ABCD中，∠ADC=∠ABC=45°,CD=,BC=,连接AC、BD,若AC⊥AB,则BD的长度为_______________.

Answer 1

【答案】

【解析】

作AE⊥AD交DC的延长线于点E，则易知△ADE为等腰Rt△，易证∠1=∠2．

由SAS定理证明△ABE≌△ACD，得到BE的长，∠4=∠ADC=45°，则∠BED=90°，由勾股定理求出EC、BD的长，从而得到结论．

作AE⊥AD交DC的延长线于点E，则易知△ADE为等腰Rt△．

∵∠1+∠3=∠2+∠3=90°，∴∠1=∠2．

∵AB=AC，∠1=∠2，AE=AD，∴△ABE≌△ACD（SAS），∴BE=CD=，∠4=∠ADC=45°，∴∠BED=90°，∴EC==，∴BD===．

故答案为：．