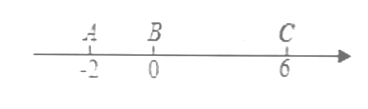题目内容
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
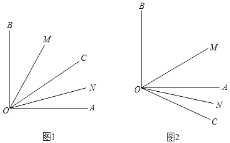
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
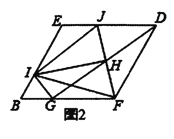
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

【答案】(1)见解析;(2)证明见解析;(3)FH=2![]() .
.
【解析】(1)先求出AB,BC,AC,再分情况求出CD或AD,即可画出图形;
(2)先判断出∠A+∠ADB=140°=∠ADC,即可得出结论;
(3)先判断出△FEH∽△FHG,得出FH2=FEFG,再判断出EQ=![]() FE,继而求出FGFE=8,即可得出结论.
FE,继而求出FGFE=8,即可得出结论.
(1)由图1知,AB=![]() ,BC=2
,BC=2![]() ,∠ABC=90°,AC=5,
,∠ABC=90°,AC=5,
∵四边形ABCD是以AC为“相似对角线”的四边形,
当∠ACD=90°时,△ACD∽△ABC或△ACD∽△CBA,
∴![]() 或
或![]() ,
,
∴CD=10或CD=2.5
同理:当∠CAD=90°时,AD=2.5或AD=10,
(2)∵∠ABC=80°,BD平分∠ABC,
∴∠ABD=∠DBC=40°,
∴∠A+∠ADB=140°
∵∠ADC=140°,
∴∠BDC+∠ADB=140°,
∴∠A=∠BDC,
∴△ABD∽△BDC,
∴BD是四边形ABCD的“相似对角线”;

(3)如图3,
∵FH是四边形EFGH的“相似对角线”,
∴△EFH与△HFG相似,
∵∠EFH=∠HFG,
∴△FEH∽△FHG,
∴![]() ,
,
∴FH2=FEFG,
过点E作EQ⊥FG于Q,
∴EQ=FEsin60°=![]() FE,
FE,
∵![]() FG×EQ=2
FG×EQ=2![]() ,
,
∴![]() FG×
FG×![]() FE=2
FE=2![]() ,
,
∴FGFE=8,
∴FH2=FEFG=8,
∴FH=2![]() .
.