题目内容
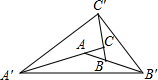
如图,将△ABC的三边AB,BC,CA分别延长至B′,C′,A′,且使BB′=AB,CC′=2BC,AA′=3AC.若S△ABC=1,那么S△A'B'C'是( )
| A.15 | B.16 | C.17 | D.18 |

连接CB',
∵AB=BB',
∴S△BB'C=S△ABC=1,又CC'=2BC,
∴S△B'CC'=2S△BB'C=2.∴S△BB'C'=3.
同理可得S△A'CC'=8,S△A'B'A=6.
∴S△A'B'C'=3+8+6+1=18.
∴故选D.
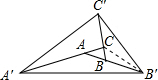
∵AB=BB',
∴S△BB'C=S△ABC=1,又CC'=2BC,
∴S△B'CC'=2S△BB'C=2.∴S△BB'C'=3.
同理可得S△A'CC'=8,S△A'B'A=6.
∴S△A'B'C'=3+8+6+1=18.
∴故选D.


练习册系列答案
相关题目