题目内容
.某私营服装厂根据2011年市场分析,决定2012年调整服装制作方案,准备每周(按120工时计算)制作西服、休闲服、衬衣共360件,且衬衣至少60件。已知每件服装的收入和所需工时如下表:
设每周制作西服x件,休闲服y件,衬衣z件。
(1)请你分别从件数和工时数两个方面用含有x,y 的代数式表示衬衣的件数z,
(2)求y与x之间的函数关系式。
(3)问每周制作西服、休闲服、衬衣各多少件时,才能使总收入最高?最高总收入是多少?
| 服装名称 | 西服 | 休闲服 | 衬衣 |
| 工时/件 |  |  |  |
| 收入(百元)/件 | 3 | 2 | 1 |
(1)请你分别从件数和工时数两个方面用含有x,y 的代数式表示衬衣的件数z,
(2)求y与x之间的函数关系式。
(3)问每周制作西服、休闲服、衬衣各多少件时,才能使总收入最高?最高总收入是多少?
(1)z=360-x-y (2)y=360-3x(3)每周生产西服30件,休闲服270件,衬衣60件时,总收入最高,最高总收入是690百元
解:(1)从件数方面:z=360-x-y,
从工时数方面:由 x+
x+ y+
y+ z=120整理得:z=480-2x-
z=120整理得:z=480-2x- y。
y。
(2)由(1)得360-x-y=480-2x- y,整理得:y=360-3x。
y,整理得:y=360-3x。
(3)由题意得总收入s=3x+2y+z=3x+2(360-3x)+2x=-x+720
由题意得 ,解得30≤x≤120。
,解得30≤x≤120。
由一次函数的性质可知,当x=30的时候,s最大,即当每周生产西服30件,休闲服270件,衬衣60件时,总收入最高,最高总收入是690百元。
(1)根据题目中的已知条件分别从件数和工时数两个方面用含x,y的关系式表示z。
(2)由(1)整理得:y=360-3x。
(3)由题意得s=3x+2y+z,化为一个自变量,得到关于x的一次函数。由题意得 ,
,
解得30≤x≤120,从而根据一次函数的性质作答。
从工时数方面:由
 x+
x+ y+
y+ z=120整理得:z=480-2x-
z=120整理得:z=480-2x- y。
y。(2)由(1)得360-x-y=480-2x-
 y,整理得:y=360-3x。
y,整理得:y=360-3x。(3)由题意得总收入s=3x+2y+z=3x+2(360-3x)+2x=-x+720
由题意得
 ,解得30≤x≤120。
,解得30≤x≤120。由一次函数的性质可知,当x=30的时候,s最大,即当每周生产西服30件,休闲服270件,衬衣60件时,总收入最高,最高总收入是690百元。
(1)根据题目中的已知条件分别从件数和工时数两个方面用含x,y的关系式表示z。
(2)由(1)整理得:y=360-3x。
(3)由题意得s=3x+2y+z,化为一个自变量,得到关于x的一次函数。由题意得
 ,
,解得30≤x≤120,从而根据一次函数的性质作答。

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目

 的图象经过点A(0,-2),B(1,0),则b= ,k= .
的图象经过点A(0,-2),B(1,0),则b= ,k= . (
( 为常数)上有两点
为常数)上有两点 和
和 ,若
,若 ,则
,则 与
与 的大小关系是( )
的大小关系是( )


 ;②
;② ;③
;③ ;④
;④ .其中一次函数的个数是()
.其中一次函数的个数是()
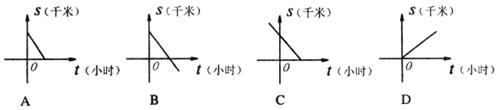
 小时后与北京的距离为
小时后与北京的距离为 千米,下列图象能大致反映
千米,下列图象能大致反映