题目内容
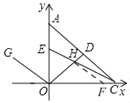
【题目】如图,以直角△AOC的直角顶点O为原点,以OC,OA所在直线为x轴和y轴建立平面直角坐标系,点A(0,a),C(b,0)满足![]() .
.

(1)点A的坐标为________;点C的坐标为________.
(2)已知坐标轴上有两动点P,Q同时出发,P点从C点出发沿x轴负方向以每秒2个单位长度的速度匀速移动,Q点从O点出发沿y轴正方向以每秒1个单位长度的速度匀速移动,点P到达O点整个运动随之结束.AC的中点D的坐标是(4,3),设运动时间为t秒.问:是否存在这样的t,使得△ODP与△ODQ的面积相等?若存在,请求出t的值;若不存在,请说明理由.
(3)在(2)的条件下,若∠DOC=∠DCO,点G是第二象限中一点,并且y轴平分∠GOD.点E是线段OA上一动点,连接接CE交OD于点H,当点E在线段OA上运动的过程中,探究∠GOA,∠OHC,∠ACE之间的数量关系,并证明你的结论(三角形的内角和为180°可以直接使用).
【答案】(1)(0,6),(8,0);(2)存在t=2.4时,使得△ODP与△ODQ的面积相等;(3)2∠GOA+∠ACE=∠OHC,理由见解析.
【解析】
(1)根据算术平方根的非负性,绝对值的非负性即可求解;
(2)根据运动速度得到OQ=t,OP=8-2t,根据△ODP与△ODQ的面积相等列方程求解即可;
(3)由∠AOC=90°,y轴平分∠GOD证得OG∥AC,过点H作HF∥OG交x轴于F,得到∠FHC=∠ACE,∠FHO=∠GOD,从而∠GOD+∠ACE=∠FHO+∠FHC,即可证得2∠GOA+∠ACE=∠OHC.
(1)∵![]() ,
,
∴a-b+2=0,b-8=0,
∴a=6,b=8,
∴A(0,6),C(8,0);
故答案为:(0,6),(8,0);
(2)由(1)知,A(0,6),C(8,0),
∴OA=6,OB=8,
由运动知,OQ=t,PC=2t,
∴OP=8-2t,
∵D(4,3),
∴![]() ,
,
![]() ,
,
∵△ODP与△ODQ的面积相等,
∴2t=12-3t,
∴t=2.4,
∴存在t=2.4时,使得△ODP与△ODQ的面积相等;
(3)2∠GOA+∠ACE=∠OHC,理由如下:
∵x轴⊥y轴,
∴∠AOC=∠DOC+∠AOD=90°,
∴∠OAC+∠ACO=90°.
又∵∠DOC=∠DCO,
∴∠OAC=∠AOD.
∵x轴平分∠GOD,
∴∠GOA=∠AOD.
∴∠GOA=∠OAC.
∴OG∥AC,
如图,过点H作HF∥OG交x轴于F,
∴HF∥AC,
∴∠FHC=∠ACE.
∵OG∥FH,
∴∠GOD=∠FHO,
∴∠GOD+∠ACE=∠FHO+∠FHC,
即∠GOD+∠ACE=∠OHC,
∴2∠GOA+∠ACE=∠OHC.

 阅读快车系列答案
阅读快车系列答案【题目】为了了解学生的课外学习负担,即墨区某中学数学兴趣小组决定对本校学生每天的课外学习情况进行调查,他们随机抽取本校部分学生进行了问卷调查,并将调查结果分为A,B,C,D四个等级,列表如下:
等级 | A | B | C | D |
每天课外学习时间 |
|
|
|
|
根据调查结果绘制了如图所示的两幅不完整的统计图,请你根据图中信息解答下列问题:

![]() 本次抽样调查共抽取了多少名学生?其中学习时间在B等级的学生有多少人?
本次抽样调查共抽取了多少名学生?其中学习时间在B等级的学生有多少人?
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 表示D等级的扇形圆心角的度数是多少?
表示D等级的扇形圆心角的度数是多少?
![]() 该校共有2000名学生,每天课外学习时间在2小时以内的学生有多少人?
该校共有2000名学生,每天课外学习时间在2小时以内的学生有多少人?