题目内容
【题目】上午8时,一条船从海岛A出发,以15海里/时的速度向正北航行,10时到达海岛B处,从A,B望灯塔C,测得∠NAC=30,∠NBC=60.

(1)求从海岛B到灯塔C的距离;
(2)这条船继续向正北航行,问在上午或下午的什么时间小船与灯塔C的距离最短?
【答案】(1)30海里 (2)上午的11时
【解析】
(1)根据已知条件得到∠ACB=60°-30°=30°,根据等腰三角形的性质得到结论;
(2)过C作CP⊥AB于P,则线段CP的长即为小船与灯塔C的最短距离,根据直角三角形的性质即可得到结论.
(1)∵∠NBC=60,∠NAC=30°,
∴∠ACB=60°-30°=30°,
∴AB=BC,
∵AB=15×2=30海里,
∴从海岛B到灯塔C的距离为30海里;
(2)过C作CP⊥AB于P,则线段CP的长即为小船与灯塔C的最短距离,
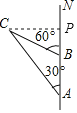
∵∠NBC=60°,∠BPC=90°,
∴∠PCB=90°-60°=30°,
∴PB=![]() BC=15海里,
BC=15海里,
∴15÷15=1小时,
∴这条船继续向正北航行,在上午11时小船与灯塔C的距离最短.

 中考解读考点精练系列答案
中考解读考点精练系列答案【题目】某学校为了解本校七年级学生期末考试数学成绩情况,决定进行抽样分析已知该校七年级共有10个班,每班40名学生,请根据要求回答下列问题:
(1)若要从全年级学生中抽取一个40人的样本,你认为以下抽样方法中比较合理的有__________.(只要填写序号).
①随机抽取一个班级的学生;
②在全年级学生中随机抽取40名男学生;
③在全年级10个班中各随机抽取4名学生.
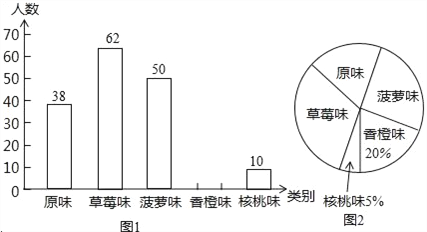
(2)将抽取的40名学生的数学成绩进行分组,并绘制频数表和成绩分布统计图(不完整),如图:
①请补充完整频数表;
成绩(分) | 频数 | 频率 |
| __________ | 0.3 |
| __________ | 0.4 |
| 8 | __________ |
| 4 | __________ |
②写出图中![]() 、
、![]() 类圆心角度数;并估计全年级
类圆心角度数;并估计全年级![]() 、
、![]() 类学生大约人数.
类学生大约人数.