Question

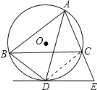
【题目】如图，已知内接于，平分，交于点，过作的切线与的延长线交于点．

求证：；

若，，求的长；

在题设条件下，为使是平行四边形，应满足怎样的条件（不要求证明）．

Answer 1

【答案】（1）证明见解析；（2）；(3)

【解析】

（1）连接CD，可根据圆周角定理通过AD平分∠BAC得出∠DCB=∠DBC，根据弦切角定理可得出∠CDE=∠DBC，将等角置换后即可得出∠BCD=∠CDE．即可得出平行；

（2）由（1）不难得出BD=CD（等角对等边），然后通过证明三角形ABD和CDE相似，来得出AB、BC、CD、CE的比例关系，有了AB、BD、CD的值就求出了CE的长；

（3）要使BDEC是平行四边形，那么BD∥CE，可通过弦切角定理得出∠BAD=∠ACB，也就得出了，上面（1）中已经得出，因此，∠ACB=∠BAD=∠CAD，因此∠BAC=2∠ACB．

（1）连接；

∵是圆的切线，

∴，

∵，

∴，

∵平分，

∴，

∴，

∵，

∴，

∴；

如图，连接；

∵平分，

∴，

∴，

∴，

∵，

∴，

又由中已证得，

∴，

∴，

∴；

应该是．