Question

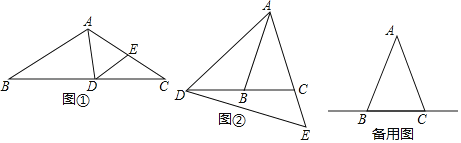
【题目】小明在学习了“等边三角形”后，激发了他的学习和探究的兴趣，就想考考他的朋友小崔，小明作了一个等边，如图1，并在边上任意取了一点（点不与点、点重合），过点作交于点，延长到，使得，连接交于点.

（1）若，求的长度；

（2）如图2，延长到，再延长到，使得，连接，，求证：.

Answer 1

【答案】（1）HI =5；(2)见解析.

【解析】

（1）作FP∥BC交AB于点P，证明是等边三角形得到AH=PH， 再证明得到PI=BI，于是可得HI =AB，即可求解；
（2）延长BD至Q，使DQ=AB，连结EQ，就可以得出BE=BQ，得出△BEQ是等边三角形，就可以得出BE=QE，得出△BCE≌△QDE就可以得出结论．

解：如图1，作FP∥BC交AB于点P，

∵是等边三角形,

∴∠ABC=∠A=60°,

∵FP∥BC,

∴∠APF=∠ABC=60°, ∠PFI=∠BGI,

∴∠APF=∠A=60°,

∴是等边三角形,

∴PF=AF,

∵，

∴AH=PH,

∵AF=BG,

∴PF=BG,

∴在和中，

,

∴,

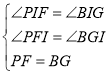∴PI=BI,

∴PI+PH=BI+AH=AB,

∴HI=PI+PH =AB= =5；

(2)如图2，延长BD至Q，使DQ=AB，连结EQ，

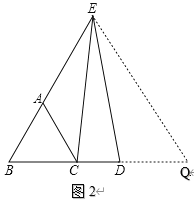
∵△ABC是等边三角形，

∴AB=BC=AC，∠B=60°．

∵AE=BD，DQ=AB，

∴AE+AB=BD+DQ，

∴BE=BQ．

∵∠B=60°，

∴△BEQ为等边三角形，

∴∠B=∠Q=60°，BE=QE．

∵DQ=AB，

∴BC=DQ．

∴在△BCE和△QDE中，

，

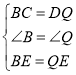∴△BCE≌△QDE（SAS），
∴EC=ED．

∴∠ECD=∠EDC.