题目内容
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,点D是边BC上的动点,连接AD,点C关于直线AD的对称点为点E,射线BE与射线AD交于点F.


(1)在图1中,依题意补全图形;
(2)记![]() (
(![]() ),求
),求![]() 的大小;(用含
的大小;(用含![]() 的式子表示)
的式子表示)
(3)若△ACE是等边三角形,猜想EF和BC的数量关系,并证明.
【答案】(1)见解析;(2)![]() ;(3)BC=2EF,证明见解析.
;(3)BC=2EF,证明见解析.
【解析】
(1)根据题意画图即可补全图形;
(2)如图3,连接AE、DE,根据轴对称的性质可得:AE=AC,∠EAD=![]() ,进而可用α的代数式表示出∠BAF,然后在等腰△ABE中利用三角形的内角和即可求出
,进而可用α的代数式表示出∠BAF,然后在等腰△ABE中利用三角形的内角和即可求出![]() ;
;
(3)如图4,设AF、CE交于点G,由△ACE是等边三角形可得∠EAC=60°,CE=AC,然后根据轴对称的性质可得AF⊥CE,∠FAE=![]() ,进而可得∠BAF=60°,CE=2EG,易证△EFG为等腰直角三角形,从而可得
,进而可得∠BAF=60°,CE=2EG,易证△EFG为等腰直角三角形,从而可得![]() ,而
,而![]() ,进一步即可得出结论.
,进一步即可得出结论.
解:(1)补全图形如图2:
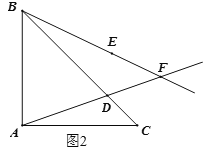
(2)如图3,连接AE、DE,
∵点C关于直线AD的对称点为点E,∴AE=AC,∠EAD=![]() ,
,
∵AB=AC,∠BAC=90°,∴AB=AE,![]() ,
,
∴![]() ;
;

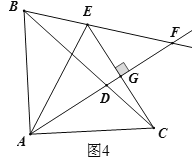
(3)猜想:BC=2EF.
证明:如图4,设AF、CE交于点G,
∵△ACE是等边三角形,∴∠EAC=60°,CE=AC,
∵点C关于直线AD的对称点为点E,
∴AF⊥CE,∠FAE=![]() ,∴∠BAF=60°,CE=2EG,
,∴∠BAF=60°,CE=2EG,
由(2)题知,∠ABF=45°+30°=75°,则在△ABF中,∠AFB=180°-∠ABF-∠BAF=45°,
∴∠GEF=45°,∴![]() ,
,
又∵AB=AC,∠BAC=90°,∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目






