题目内容
【题目】如图1,直线y=﹣![]() x+4与坐标轴分别相交于A、B两点,在第一象限内,以线段AB为边向外作正方形ABCD,过A、C点作直线AC.
x+4与坐标轴分别相交于A、B两点,在第一象限内,以线段AB为边向外作正方形ABCD,过A、C点作直线AC.

(1)填空:点A的坐标是 ,正方形ABCD的边长等于 ;
(2)求直线AC的函数解析式;
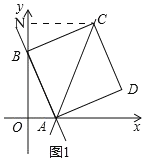
(3)如图2,有一动点M从B出发,以1个单位长度/秒的速度向终点C运动,设运动的时间为t(秒),连接AM,当t为何值时,则AM平分∠BAC?请说明理由.
【答案】(1)(3,0),5;(2)y=7x﹣21;(3)t为5![]() ﹣5时,AM平分∠BAC.
﹣5时,AM平分∠BAC.
【解析】
(1)根据坐标轴上点的特点求出点A,B坐标,即可得出结论;(2)先判断出△AOB≌△BNC,得出BN=OA=3,CN=OB=4,即可求出点C纵坐标,最后用待定系数法即可得出结论;(3)先判断出MF=CF,用CM=![]() BM建立方程即可得出结论;
BM建立方程即可得出结论;
解:
(1)∵直线y=![]() 与坐标轴分别相交于A、B两点,
与坐标轴分别相交于A、B两点,
令x=0,则y=4,
∴B(0,4),
令y=0,则0=![]() ,
,
∴x=3,
∴A(3,0),
∴AB=![]() =5,
=5,
故答案为:(3,0),5;
(2)如图1,过点C作CN⊥OB于N,
∴∠CBN+∠BCN=90°,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠OBA+∠CBN=90°,
∴∠OBA=∠BCN,
在△AOB和△BNC中,
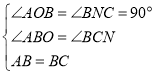 ,
,
∴△AOB≌△BNC(AAS),
∴CN=OB=4,BN=OA=3,
∴ON=OB+BN=7,
∴C(4,7),
设直线AC的解析式为y=kx+b,
∵A(3,0),
∴![]() ,
,
∴![]() ;
;
∴直线AC的解析式为y=7x﹣21;
(3)如图2,过M作MF⊥AC
当AM为∠BAC的角平分线时,
∵MF⊥AC,MB⊥AB
∴BM=FM
∵∠MCF=45°,
∴MF=CF
设BM=x,则CM=5﹣x,
则CM=![]() MF=
MF=![]() BM,
BM,
∴5﹣x=![]() x,
x,
∴(![]() +1)x=5,
+1)x=5,
∴x=![]() ,
,
∴t为![]() 时,AM平分∠BAC.
时,AM平分∠BAC.

【题目】蜀山区植物园是一座三面环水的半岛园区,拥有梅园、桂花园、竹园、木兰园、水景园等示范区。为了种植植物,需要从甲乙两地向园区A,B两个大棚配送营养土,已知甲地可调出50吨营养土,乙地可调出80吨营养土,A棚需70吨营养土,B棚需60吨营养土,甲乙两地运往A,B两棚的运费如下表所示(表中运费栏“元/吨”表示运送每吨营养土所需费用)。
运费(元/吨) | ||
A | B | |
甲地 | 12 | 12 |
乙地 | 10 | 8 |
运往A、B两地的吨数 | ||
A | B | |
甲地 | x | 50-x |
乙地 | ( ) | ( ) |
(1)设甲地运往A棚营养土x吨,请用关于x的代数式完成上表;
(2)设甲地运往A棚营养土x吨,求总运费y(元)关于x(吨)的函数关系式(要求写出变量取值范围);
(3)当甲、乙两地各运往A、B两棚多少吨营养土时,总运费最省?最省的总运费是多少?





