题目内容
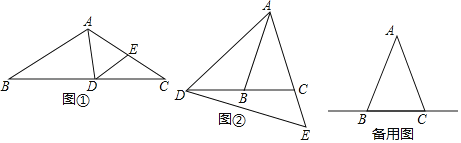
【题目】△ABC中，最小内角∠B＝24°，若△ABC被一直线分割成两个等腰三角形，如图为其中一种分割法，此时△ABC中的最大内角为90°，那么其它分割法中，△ABC中的最大内角度数为_____．
【答案】117°或108°或84°．
【解析】
根据等腰三角形的性质进行分割，写出△ABC中的最大内角的所有可能值.
①∠BAD＝∠BDA＝
（180°﹣24°）＝78°，∠DAC＝∠DCA＝∠BDA＝39°，如图1所示：
∴∠BAC＝78°+39°＝117°；
②∠DBA＝∠DAB＝24°，∠ADC＝∠ACD＝2∠DBA＝48°，如图2所示：
∴∠DAC＝180°﹣2×48°＝84°，
∴∠BAC＝24°+84°＝108°；
③∠DBA＝∠DAB＝24°，∠ADC＝∠DAC＝2∠DBA＝48°，如图3所示：
∴∠BAC＝24°+48°＝72°，∠C＝180°﹣2×48°＝84°；
∴其它分割法中，△ABC中的最大内角度数为117°或108°或84°，
故答案为：117°或108°或84°．
【题目】蜀山区植物园是一座三面环水的半岛园区，拥有梅园、桂花园、竹园、木兰园、水景园等示范区。为了种植植物，需要从甲乙两地向园区A，B两个大棚配送营养土，已知甲地可调出50吨营养土，乙地可调出80吨营养土，A棚需70吨营养土，B棚需60吨营养土，甲乙两地运往A，B两棚的运费如下表所示（表中运费栏“元/吨”表示运送每吨营养土所需费用）。
运费（元/吨） | ||
A | B | |
甲地 | 12 | 12 |
乙地 | 10 | 8 |
运往A、B两地的吨数 | ||
A | B | |
甲地 | x | 50-x |
乙地 | （ ） | （ ） |
（1）设甲地运往A棚营养土x吨，请用关于x的代数式完成上表；
（2）设甲地运往A棚营养土x吨，求总运费y（元）关于x（吨）的函数关系式（要求写出变量取值范围）；
（3）当甲、乙两地各运往A、B两棚多少吨营养土时，总运费最省？最省的总运费是多少？
