题目内容
如图,C(0,3),过点C开口向下的抛物线交x轴于点A、B(点A在点B的右边),已知∠CB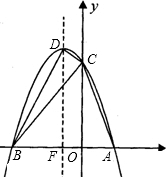 A=45°,tanA=3;
A=45°,tanA=3;
(1)求A、B两点坐标;
(2)求抛物线解析式及抛物线顶点D的坐标;
(3)E(0,m)为y轴上一动点(不与点C重合)
①当直线EB与△BCD外接圆相切时,求m的值;
②指出点E的运动过程中,∠DEC与∠DBC的大小关系及相应m的取值范围.
 A=45°,tanA=3;
A=45°,tanA=3;(1)求A、B两点坐标;
(2)求抛物线解析式及抛物线顶点D的坐标;
(3)E(0,m)为y轴上一动点(不与点C重合)
①当直线EB与△BCD外接圆相切时,求m的值;
②指出点E的运动过程中,∠DEC与∠DBC的大小关系及相应m的取值范围.
(1)∵C(0,3)
∴OC=3
∵∠CBA=45°
∴OC=OB=3
∵tanA=3
∴
=3,即
=3
∴OA=1
∴A(1,O),B(-3,0)
(2)设抛物线的解析式为:y=a(x-1)(x+3)
把C(0,3)代入得-3a=3
∴a=-1
∴y=-(x-1)(x+3)
y=-x2-2x+3
∴-
=-1,
=4
∴D(-1,4)
(3)①作DH⊥y轴于H,则DH=1,CH=OH-OC=1
由勾股定理得:CD=
,CD2=2
在△BOC中,由勾股定理得,BC=
OC
∴BC=3
,BC2=18
在Rt△BDF中,BF=BO-OF=2,DF=4,由勾股定理得;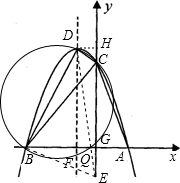
BD=2
∴DB2=20
在△BCD中∴CD2+BC2=DB2
∴△BCD是直角三角形.
∴BD是△BCD的外接圆的直径
∵BE与△BCD的外接圆相切
∴BE⊥BD
∴∠DBE=90°
∴∠EBO=∠BDF
∴△BDF∽△EBO
∴
=
即
=
∴OE=
∴E(0,-
)
即m=-
②当点E在C点的上方时,当∠DEC=∠DBC时,
∵∠DHE=∠DCB=90°
∴△DEH∽△DBC
∴
=
=3
∴EH=3,OE=EH+HO=7
∴E(0,7)
∴当m=7时,∠DEC=∠DBC
当m>时,∠DEC<∠DBC
当m<7时,∠DEC>∠DBC
点E在C下方时,同理可得当∠DEC=∠DBC时,EH=3
∴此时OE=4-3=1
∴E(0,1)
∴当m=1时,∠DEC=∠DBC
当1<m<3时,∠DEC>∠DBC
当m<1时,∠DEC<∠DBC
综上所述得:m>7或m<1时,∠DEC<∠DBC
m=7或m=1时,∠DEC=∠DBC
1<m<7且m≠3时,∠DEC>∠DBC
∴OC=3
∵∠CBA=45°
∴OC=OB=3
∵tanA=3
∴
| OC |
| OA |
| 3 |
| OA |
∴OA=1
∴A(1,O),B(-3,0)
(2)设抛物线的解析式为:y=a(x-1)(x+3)
把C(0,3)代入得-3a=3
∴a=-1
∴y=-(x-1)(x+3)
y=-x2-2x+3
∴-
| b |
| 2a |
| 4ac-b2 |
| 4a |
∴D(-1,4)
(3)①作DH⊥y轴于H,则DH=1,CH=OH-OC=1
由勾股定理得:CD=
| 2 |
在△BOC中,由勾股定理得,BC=
| 2 |
∴BC=3
| 2 |
在Rt△BDF中,BF=BO-OF=2,DF=4,由勾股定理得;

BD=2
| 5 |
在△BCD中∴CD2+BC2=DB2
∴△BCD是直角三角形.
∴BD是△BCD的外接圆的直径
∵BE与△BCD的外接圆相切
∴BE⊥BD
∴∠DBE=90°
∴∠EBO=∠BDF
∴△BDF∽△EBO
∴
| OE |
| BF |
| OB |
| DF |
| OE |
| 2 |
| 3 |
| 4 |
∴OE=
| 3 |
| 2 |
∴E(0,-
| 3 |
| 2 |
即m=-
| 3 |
| 2 |
②当点E在C点的上方时,当∠DEC=∠DBC时,
∵∠DHE=∠DCB=90°
∴△DEH∽△DBC
∴
| EH |
| DH |
| BC |
| DC |
∴EH=3,OE=EH+HO=7
∴E(0,7)
∴当m=7时,∠DEC=∠DBC
当m>时,∠DEC<∠DBC
当m<7时,∠DEC>∠DBC
点E在C下方时,同理可得当∠DEC=∠DBC时,EH=3
∴此时OE=4-3=1
∴E(0,1)
∴当m=1时,∠DEC=∠DBC
当1<m<3时,∠DEC>∠DBC
当m<1时,∠DEC<∠DBC
综上所述得:m>7或m<1时,∠DEC<∠DBC
m=7或m=1时,∠DEC=∠DBC
1<m<7且m≠3时,∠DEC>∠DBC

练习册系列答案
相关题目



 的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.
的速度向点B运动.若点M、N同时开始运动,其中一点到达终点,另一点也停止运动,运动时间为t(t>0).过点N作NP⊥BC与P,交BD于点Q.