题目内容
在平面直角坐标系xOy中,抛物线的解析式是y=
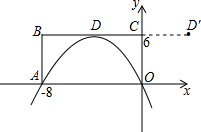
x2+1,点C的坐标为(-4,0),平行四边形OABC的顶点A,B在抛物线上,AB与y轴交于点M,已知点Q(x,y)在抛物线上,点P(t,0)在x轴上.
(1)写出点M的坐标;
(2)当四边形CMQP是以MQ,PC为腰的梯形时.
①求t关于x的函数解析式和自变量x的取值范围;
②当梯形CMQP的两底的长度之比为1:2时,求t的值.

| 1 |
| 4 |
(1)写出点M的坐标;
(2)当四边形CMQP是以MQ,PC为腰的梯形时.
①求t关于x的函数解析式和自变量x的取值范围;
②当梯形CMQP的两底的长度之比为1:2时,求t的值.

(1)∵OABC是平行四边形,∴AB∥OC,且AB=OC=4,
∵A,B在抛物线上,y轴是抛物线的对称轴,
∴A,B的横坐标分别是2和-2,
代入y=
x2+1得,A(2,2),B(-2,2),
∴M(0,2),(2分)
(2)①过点Q作QH⊥x轴,连接MC.
∵CM∥PQ,
∴∠QPC=∠MCO,
∵∠COM=∠PHQ=90°,
∴△HQP∽△OMC,
设垂足为H,则HQ=y,HP=x-t,
由△HQP∽△OMC,得:
=
,即:t=x-2y,
∵Q(x,y)在y=
x2+1上,
∴t=-
x2+x-2.(2分)
当点P与点C重合时,梯形不存在,此时,t=-4,解得x=1±
,
当Q与B或A重合时,四边形为平行四边形,此时,x=±2
∴x的取值范围是x≠1±
,且x≠±2的所有实数;(2分)
②分两种情况讨论:
(1)当CM>PQ时,则点P在线段OC上,
∵CM∥PQ,CM=2PQ,
∴点M纵坐标为点Q纵坐标的2倍,即2=2(
x2+1),解得x=0,
∴t=-
02+0-2=-2;(2分)
(2)当CM<PQ时,则点P在OC的延长线上,
∵CM∥PQ,CM=
PQ,
∴点Q纵坐标为点M纵坐标的2倍,即
x2+1=2×2,
解得:x=±2
;(2分)
当x=-2
时,得t=-
(2
)2-2
-2=-8-2
,
当x=2
时,得t=2
-8.
∵A,B在抛物线上,y轴是抛物线的对称轴,
∴A,B的横坐标分别是2和-2,
代入y=
| 1 |
| 4 |
∴M(0,2),(2分)
(2)①过点Q作QH⊥x轴,连接MC.
∵CM∥PQ,
∴∠QPC=∠MCO,
∵∠COM=∠PHQ=90°,
∴△HQP∽△OMC,
设垂足为H,则HQ=y,HP=x-t,

由△HQP∽△OMC,得:
| y |
| 2 |
| x-t |
| 4 |
∵Q(x,y)在y=
| 1 |
| 4 |
∴t=-
| 1 |
| 2 |
当点P与点C重合时,梯形不存在,此时,t=-4,解得x=1±
| 5 |
当Q与B或A重合时,四边形为平行四边形,此时,x=±2
∴x的取值范围是x≠1±
| 5 |
②分两种情况讨论:
(1)当CM>PQ时,则点P在线段OC上,
∵CM∥PQ,CM=2PQ,
∴点M纵坐标为点Q纵坐标的2倍,即2=2(
| 1 |
| 4 |
∴t=-
| 1 |
| 2 |
(2)当CM<PQ时,则点P在OC的延长线上,
∵CM∥PQ,CM=
| 1 |
| 2 |
∴点Q纵坐标为点M纵坐标的2倍,即
| 1 |
| 4 |
解得:x=±2
| 3 |
当x=-2
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
当x=2
| 3 |
| 3 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 A=45°,tanA=3;
A=45°,tanA=3;