题目内容
一名学生推铅球,铅球行进高度y(m)与水平距离x(m)之间的函数关系为y=-
x2+
x+
.
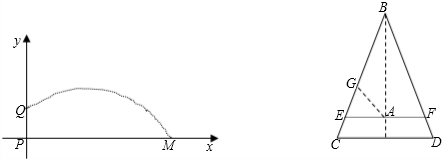
(1)画出函数的图象.
(2)观察图象,指出铅球推出的距离.
| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |
(1)画出函数的图象.
(2)观察图象,指出铅球推出的距离.
(1)用配方法求出顶点坐标与对称轴,
y=-
x2+
x+
,
=-
(x2-8x-20),
=-
[(x2-8x+16)-36],
=-
(x-4)2+3,
所以对称轴为x=4,顶点坐标为(4,3),
求与x轴的交点坐标即y=0得:
0=-
(x-4)2+3,
解得:x1=-2,x2=10,
即与x轴的交点坐标为(-2,0)(10,0),
求与y轴交点坐标,即x=0,解得:y=
,与y轴交点坐标为(0,
),
把以上各点在坐标系中描出,即是我们所要图象;
(2)由图象的可得与y轴交点坐标就是这位同学的身高,
所推铅球距离就是图象与x轴交点坐标的正值就是铅球距离,
所以铅球推出的距离是10米.

y=-
| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |
=-
| 1 |
| 12 |
=-
| 1 |
| 12 |
=-
| 1 |
| 12 |
所以对称轴为x=4,顶点坐标为(4,3),
求与x轴的交点坐标即y=0得:
0=-
| 1 |
| 12 |
解得:x1=-2,x2=10,
即与x轴的交点坐标为(-2,0)(10,0),
求与y轴交点坐标,即x=0,解得:y=
| 5 |
| 3 |
| 5 |
| 3 |
把以上各点在坐标系中描出,即是我们所要图象;
(2)由图象的可得与y轴交点坐标就是这位同学的身高,
所推铅球距离就是图象与x轴交点坐标的正值就是铅球距离,
所以铅球推出的距离是10米.


练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
 A=45°,tanA=3;
A=45°,tanA=3;