题目内容
【题目】我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.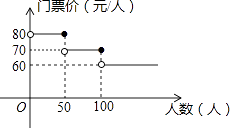
(1)求W关于x的函数关系式,并写出自变量x的取值范围;
(2)若甲团队人数不超过100人,请说明甲、乙两团队联合购票比分别购票最多可可节约多少钱;
(3)“五一”小黄金周之后,该风景区对门票价格作了如下调整:人数不超过50人时,门票价格不变;人数超过50人但不超过100人时,每张门票降价a元;人数超过100人时,每张门票降价2a元,在(2)的条件下,若甲、乙两个旅行团队“五一”小黄金周之后去游玩,甲乙两团队联合购票比分别购票最多节约3400元,求a的值.
【答案】
(1)解:∵甲团队人数为x人,乙团队人数不超过50人,
∴120﹣x≤50,
∴x≥70,
①当70≤x≤100时,W=70x+80(120﹣x)=﹣10x+9600,
②当100<x<120时,W=60x+80(120﹣x)=﹣20x+9600,
综上所述,W= ![]()
(2)解:∵甲团队人数不超过100人,
∴x≤100,
∴W=﹣10x+9600,
∵70≤x≤100,
∴x=70时,W最大=8900(元),
两团联合购票需120×60=7200(元),
∴最多可节约8900﹣7200=1700(元)
(3)解:∵x≤100,
∴W=(70﹣a)x+80(120﹣x)=﹣(a+10)x+9600,
∴x=70时,W最大=﹣70a+8900(元),
两团联合购票需120(60﹣2a)=7200﹣240a(元),
∵﹣70a+8900﹣(7200﹣240a)=3400,
解得:a=10
【解析】(1)根据题意可得到甲团队人数大于等于70,然后再分为70≤x≤100和100<x<120两种情况求解即可;
(2)由题意可知x≤100,则W=-10x+9600(70≤x≤100)然后再利用一次函数的图象和性质求得W的最大值即可;
(3)由每张门票降价a元,可得到W=(70-a)x+80(120-x)=-(a+10)x+9600,由一次函数的增减性可知:x=70时,W最大=-70a+8900(元),接下来,再求得两队团联合购票所需的费用,最后,依据甲乙两团队联合购票比分别购票最多节约3400元列方程求解即可.

 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案