题目内容
【题目】问题探究
（1）请在图①的正方形ABCD的对角线BD上作一点P，使PA+PC最小；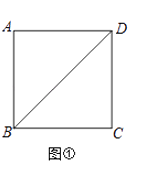
（2）如图②，点P为矩形ABCD的对角线BD上一动点，AB=2，BC=2 
，点E为BC边的中点，求作一点P，使PE+PC最小，并求这个最小值．
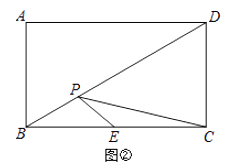
（3）如图③，李师傅有一块边长为1000米的菱形ABCD采摘园，AC=1200米，BD为小路，BC的中点E为一水池，李师傅现在准备在小路BD上建一个游客临时休息纳凉室P，为了节省土地，使休息纳凉室P到水池E与大门C的距离之和最短，那么是否存在符合条件的点P？若存在，请作出的点P位置，并求出这个最短距离；若不存在，请说明理由．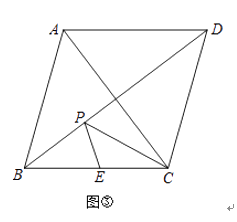
【答案】
（1）解：如图①，
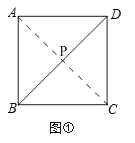
连接AC交BD于P，则AP+CP最小=AC
（2）解：如图②，作点C关于BD的对称点C'交BD于F，连接C'E交BD于P，则PE+PC最小=C'E．
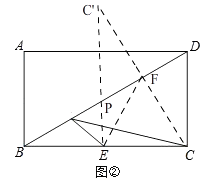
∵BD是矩形ABCD的对角线，
∴CD=AB=2，∠BCD=90°，
在Rt△BCD中，CD=2，BC=2 
，
∴tan∠CBD= 
= 
= 
，
∴∠CBD=30°，
由对称知，CC'=2CF，CC'⊥BD，
∴∠CFD=90°，
∴∠BCF=60°，∠DCF=30°，
在Rt△CDF中，CD=2，∠DCF=30°，
∴CF= ，
∴CC'=2CF=2 ，
∵点E为BC边的中点，
∴CE= 
BC= ，
∴CF=CE，
连接EF，
∴△CEF是等边三角形，
∴EF=CF=C'F，
∴△CEC'是直角三角形，
在Rt△CEC'中，CC'=2 ，CE= ，
∴C'E=3，
∴PE+PC最小为3
问题解决
（3）解：如图③，菱形ABCD的对角线相交于点O，
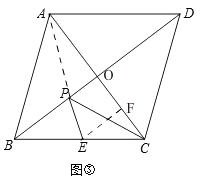
∴OC=OA= AC=600，AC⊥BD，
在Rt△BOC中，OB= 
=800，
过点E作EF⊥AC于F，
∴EF∥OB，
∵点E是BC的中点，EF= OB=400，
∵CE= BC=500，
根据勾股定理得，CF= 
=300，
∴AF=AC﹣CF=1200﹣300=900，
连接AE交BD于P，
即：PC+PE最小=AE，
在Rt△AEF中，根据勾股定理得，AE= 
=100 
，
【解析】（1）依据连点之间线段最短可知当点P在AC和BD的交点处AP+PC有最小值；
（2）作点C关于BD的对称点C'交BD于F，连接C'E交BD于P，则PE+PC最小=C'E，然后再证明△CEC'是直角三角形，最后，再利用勾股定理求解即可；；
（3）连接AE交BD于P，过点E作EF⊥AC，再利用三角形的中位线求出EF，接下来，再利用勾股定理求出CF，最后在Rt△AEF中利用勾股定理即可．
【考点精析】关于本题考查的菱形的性质，需要了解菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半才能得出正确答案．
