��Ŀ����
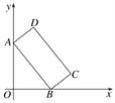
����Ŀ����ͼ1������ԭ���������y=ax2+bx+c��x�����һ������Ϊ��C����˫����y= ![]() �ཻ�ڵ�A��B��ֱ��AB��ֱ���x�ᡢy�ύ�ڵ�D��E����֪��A������Ϊ����1��4������B�ڵ����������ҵ�x�ᡢy��ľ�����ȣ�
�ཻ�ڵ�A��B��ֱ��AB��ֱ���x�ᡢy�ύ�ڵ�D��E����֪��A������Ϊ����1��4������B�ڵ����������ҵ�x�ᡢy��ľ�����ȣ�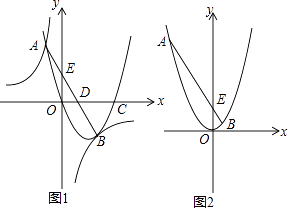
��1����˫���ߺ������ߵĽ���ʽ��
��2�������ABC�������
��3����ͼ2����������ƽ����������ԭ����ʱ��ֱ��AB��֮ƽ�ƣ����жϣ���y��ĸ��������Ƿ���ڵ�P��ʹ��PAB������Բ��Բ����y���ϣ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺�ѵ�A���������˫���ߵĽ���ʽ�ã�k=��1��4=��4��
����˫���ߵĽ���ʽΪy=�� ![]() ��
��
���B��������m����m����
�ߵ�B��˫�����ϣ�
�ੁm2=��4�����m=2��m=��2��
�ߵ�B�ڵ������ޣ�
��m=2��
��B��2����2����
����A��B��C���������ã� 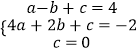 ��
��
��ã� 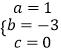 ��
��
�������ߵĽ���ʽΪy=x2��3x��
��2���⣺��ͼ1������AC��BC��
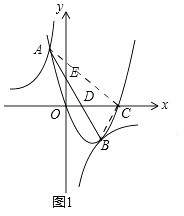
��y=0����x2��3x=0��
��x=0��x=3��
��C��3��0����
��A����1��4����B��2����2����
��ֱ��AB�Ľ���ʽΪy=��2x+2��
�ߵ�D��ֱ��AB��x��Ľ��㣬
��D��1��0����
��S��ABC=S��ADC+S��BDC= ![]() ��2��4+
��2��4+ ![]() ��2��2=6��
��2��2=6��
��3���⣺���ڣ����ɣ���ͼ2��
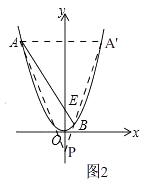
��ԭ�����ߵĽ���ʽΪy=x2��3x=��x�� ![]() ��2��
��2�� ![]() ��
��
��ԭ�����ߵĶ�������Ϊ�� ![]() ����
���� ![]() ����
����
������������ƽ�� ![]() ����λ��������ƽ��
����λ��������ƽ�� ![]() ����λ��
�����
��ƽ��ǰA����1��4����B��2����2����
��ƽ�ƺ��A���� ![]() ��
�� ![]() ����B��
����B�� ![]() ��
�� ![]() ����
����
���A����y��ĶԳƵ�A'�� ![]() ��
�� ![]() ����
����
����A'B���ӳ���y���ڵ�P������AP��
�ɶԳ���֪����APE=��BPE��
���APB������Բ��Բ����y���ϣ�
��B�� ![]() ��
�� ![]() ����A'��
����A'�� ![]() ��
�� ![]() ����
����
��ֱ��A'B�Ľ���ʽΪy=3x�� ![]() ��
��
��P��0���� ![]() ����
����
����������1�����Ƚ���A��������뷴���������Ľ���ʽ���k��ֵ��Ȼ�������B��ֵ�������ݵ�A���������˫���ߵĽ���ʽ�������ó���B�����꣬�����A��B��O�����������������ߵĽ���ʽ�����a��b��c��ֵ���ɣ�
��2���ɵ�A�͵�B����������ֱ��AB�Ľ���ʽ��Ȼ��y=0����õ�D�ĺ����꣬����������ε��������⼴�ɣ�
��3����ȷ����ƽ�ƺ��A��B�����꣬���������A����y��ĶԳƵ�����꣬���ֱ��BA'�Ľ���ʽ���ɵó���P������.

 ���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�
���Ŀ��ּ�����ҵ�����ҵ����������ϵ�д�����Ŀ�����������Ѿ���Ϊ�����ձ��ע�Ļ��⣬����������Ӱ�����ǵij��У���Ӱ�������ǵĽ�������2017��2����ĩ��Ϣ�ڼ䣬ijУ���꼶һ���ۺ�ʵ��С���ͬѧ�ԡ�������������Ҫ����Ϊ���⣬���������̫ԭ�в�������Ĺ۵㣬���Ե��������������������������²�������ͳ�Ʊ���ͳ��ͼ���۲첢�ش��������⣺
��� | ������������Ҫ���� | �ٷֱ� |
A | ��ҵ��Ⱦ | 45% |
B | ����β���ŷ� | m |
C | ���д�ȼú���� | 15% |
D | �������̻�����ȣ� | n |
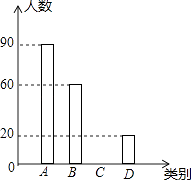
��1������������α����������������m��n��ֵ������ȫ����ͳ��ͼ��
��2����������800���˿ڣ�������Ƴ���B��C������������ж����ˣ�
��3��С��ͬѧ���ĸ��ʵء���С����״����ȫ��ͬ��С���ϱ��A��B��C��D�����ĸ�������������Ҫ�����У�����һ�������ĺ����У����������ȡһ��С�Ż�ȥ���������ȡһ��С�����û���״ͼ���б��ķ��������Сӱͬѧ�պó鵽B��D�ĸ��ʣ�����A��B��C��D��ʾ����Ŀ��