题目内容
【题目】如图,△ABC是等边三角形,点E,F分别在BC,AC上,且BE=CF,连结AE与BF相交于点G.将△ABC沿AB边折叠得到△ABD,连结DG.延长EA到点H,使得AH=BG,连结DH.
(1)求证:四边形DBCA是菱形.
(2)若菱形DBCA的面积为8 ![]() ,
, ![]() ,求△DGH的面积.
,求△DGH的面积.
【答案】
(1)证明:∵△ABC是等边三角形,
∴AC=BC由折叠知AC=AD,BC=BD,
∴AC=AD=BC=BD,
∴四边形DBCA是菱形
(2)解:∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠C=60°,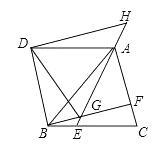
在△ABE与△BCF中,
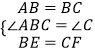 ,
,
∴△ABE≌△BCF(SAS),
∴∠AEB=∠BFC,
∵四边形DBCA是菱形,
∴DA∥BC,DB∥AC,∠BDA=∠C=60°,
∴∠HAD=∠AEB,∠DBG=∠BFC,
∴∠HAD=∠DBG,
在△DBG与△DAH中,
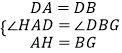 ,
,
∴△DBG≌△DAH(SAS),
∴DG=DH,∠BDG=∠ADH,
∴∠HDG=∠ADH+∠GDA=∠BDG+∠GDA=∠BDA=60°,
又∵DA=DB,DG=DH,
∴△DBA∽△DGH,
∴ ![]() ,
,
∵S△DBA= ![]() S菱形DBCA=
S菱形DBCA= ![]() ,
,
∴S△DGH= ![]()
【解析】(1)由△ABC是等边三角形和轴对称易得四边相等,证得四边形DBCA是菱形。
(2)由(1)中菱形DBCA易得△ABE≌△BCF从而利用等边三角形等量代换可得∠HAD=∠DBG,为证明△DBG≌△DAH做好条件,得到∠BDG=∠ADH最终可得△DBA∽△DGH;再利用相似三角形的面积比等于相似比的平方可得S△DGH。
【考点精析】根据题目的已知条件,利用菱形的性质和菱形的判定方法的相关知识可以得到问题的答案,需要掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案