Question

【题目】如图1，正方形ABCD的边长为8，⊙O经过点C和点D，且与AB相切于点E．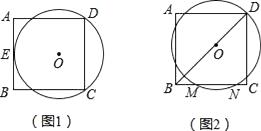

（1）求⊙O的半径；
（2）如图2，平移⊙O，使点O落在BD上，⊙O经过点D，BC与⊙O交于M，N，求MN2的值．

Answer 1

【答案】
（1）解：连接EO，延长EO交CD于F，连接DO，设半径为x．

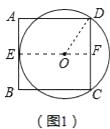
∵AB切○O于E，

∴EF⊥AB，

∵AB∥CD，

∴EF⊥CD，

∴∠OFD=90°，

在Rt△DOF中，∵∠OFD=90°，OF2+DF2=OD2，

∴x2=（8﹣x）2+42，

∴x=5，

∴⊙O的半径为5

（2）解：如图2中，作OP⊥BC于P，连接ON，则OD=ON=5，

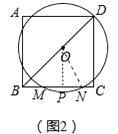
∵四边形ABCD是正方形，

∴BD=8 ，OB=BD﹣OD=8 ﹣5，OP= =8﹣ ，

∴PN2=ON2﹣OP2=52﹣（8﹣ ）2=40 ﹣51.5，

∵MN=2PN，

∴MN2=4PN2=4（40 ﹣51.5）=160 ﹣206

【解析】（1）连接EO，延长EO交CD于F，连接DO，设半径为x．根据切线的性质知EF⊥AB，根据平行线的性质及垂直的定义得出∠OFD=90°，在Rt△DOF中利用勾股定理列出方程求出解，即得到该圆的半径；
（2）如图2中，作OP⊥BC于P，连接ON，根据同圆的半径相等得OD=ON=5，根据正方形的性质及勾股定理得出BD的长，进而得出OB,根据平行线分线段成比例得出OP的长，根据勾股定理得出PN2=ON2﹣OP2，从而列出方程求出PN的长，最后根据垂径定理得出MN的长算出答案。
【考点精析】通过灵活运用平行线的判定与性质和正方形的性质，掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题．