题目内容
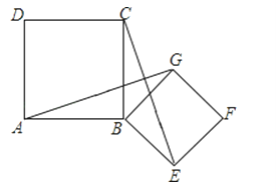
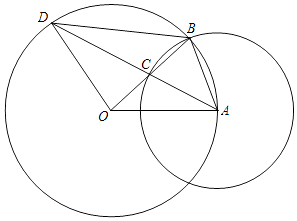
【题目】综合与实践:在综合实践课上,老师让同学们在已知三角形的基础上,经过画图,探究三角形边之间存在的关系.如图,已知点![]() 在
在![]() 的边
的边![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 且
且![]() ,在
,在![]() 上截取
上截取![]() ,再作
,再作![]() 交线段
交线段![]() 于点
于点![]() .
.

实践操作
(1)尺规作图:作出符合上述条件的图形;
探究发现
(2)勤奋小组在作出图形后,发现![]() ,
,![]() ,请说明理由;
,请说明理由;
探究应用
(3)缜密小组在勤奋小组探究的基础上,测得![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(1)见解析;(2)见解析;(3)线段![]() 的长为9
的长为9
【解析】
(1)以![]() 为圆心,任意为半径画弧,交
为圆心,任意为半径画弧,交![]() 于
于![]() ,以
,以![]() 为圆心,同等长为半径画弧,交
为圆心,同等长为半径画弧,交![]() 于
于![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径,与前弧交于
为半径,与前弧交于![]() ,连接
,连接![]() 并延长至
并延长至![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径,与
长为半径,与![]() 交于
交于![]() ,以
,以![]() 为圆心,任意长为半径画弧交
为圆心,任意长为半径画弧交![]() 于点
于点![]() ,以
,以![]() 为圆心,同等长为半径,交
为圆心,同等长为半径,交![]() 于
于![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径交前弧于
长为半径交前弧于![]() ,连接
,连接![]() 并延长交
并延长交![]() 于
于![]() ;
;
(2)根据平行和(1)中作的图证明![]() ,根据全等得出对应边相等、再根据对应角相等得出平行;
,根据全等得出对应边相等、再根据对应角相等得出平行;
(3)由(2)的全等得出![]() ,再根据线段之间的关系算出
,再根据线段之间的关系算出![]() .
.
(1)以![]() 为圆心,任意为半径画弧,交
为圆心,任意为半径画弧,交![]() 于
于![]() ,以
,以![]() 为圆心,同等长为半径画弧,交
为圆心,同等长为半径画弧,交![]() 于
于![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径,与前弧交于
为半径,与前弧交于![]() ,连接
,连接![]() 并延长至
并延长至![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径,与
长为半径,与![]() 交于
交于![]() ,以
,以![]() 为圆心,任意长为半径画弧交
为圆心,任意长为半径画弧交![]() 于点
于点![]() ,以
,以![]() 为圆心,同等长为半径,交
为圆心,同等长为半径,交![]() 于
于![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径交前弧于
长为半径交前弧于![]() ,连接
,连接![]() 并延长交
并延长交![]() 于
于![]() ,如图为所求图形:
,如图为所求图形:

(2)理由如下:
在![]() 和
和![]() 中,
中,

∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
(3)由(2)得,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴线段![]() 的长为9.
的长为9.

练习册系列答案
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目