Question

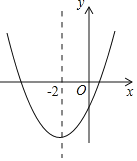
【题目】在平面直角坐标系xOy中，一次函数y=-x+k的图象与反比例函数y=-的图象交于点A（-4，n）和点B．

（1）求k的值和点B的坐标；

（2）若P是x轴上一点，且AP=AB，直接写出点P的坐标．

Answer 1

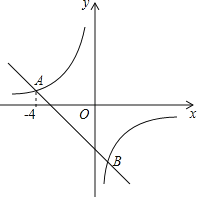
【答案】（1）点B的坐标是（1，-4）．（2）点P的是坐标（3，0）或（-11，0）．

【解析】

（1）将点A的坐标带入反比例函数解析式中，求出n值，再将A点的坐标带入一次函数解析式中即可求出k值，联立一次函数解析式与反比例函数解析式成方程组，解方程组即可得出结论；
（2）设出点P的坐标为（m，0）．根据两点间的距离公式表示出线段AP和AB的长度，根据AP=AB得出关于m的一元二次方程，解方程即可得出结论．

解：（1）把A（-4，n）代入中，

得：n=-=1，

把A（-4，1）代入y=-x+k中，

得：1=-（-4）+k，解得：k=-3．

解方程组，得或．

∴点B的坐标是（1，-4）．

（2）设点P的坐标为（m，0）．

则：AB==5，AP=．

∵AP=AB，

∴5=，即m2+8m-33=0，

解得：m1=-11，m2=3．

答：点P的是坐标（3，0）或（-11，0）．