题目内容
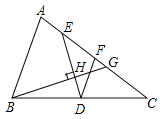
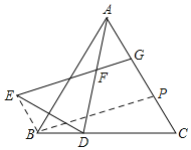
【题目】如图,在等边三角形ABC中,点D为BC边上的一点,点D关于直线AB的对称点为点E,连接AD、DE,在AD上取点F,使得∠EFD=60°,射线EF与AC交于点G.
(1)设∠BAD=α,求∠AGE的度数(用含α的代数式表示);
(2)用等式表示线段CG与BD之间的数量关系,并证明.

【答案】(1)60°+α;(2)CG=2BD,证明见解析.
【解析】
(1)根据等边三角形的性质和三角形的内角和定理可得结论;
(2)作辅助线,构建全等三角形,证明四边形EBPG是平行四边形,得BE=PG,再证明△ABD≌△BCP(AAS),可得结论.
解:(1)∵△ABC是等边三角形,
∴∠BAC=60°,
∵∠BAD=α,
∴∠FAG=60°-α,
∵∠AFG=∠EFD=60°,
∴∠AGE=180°-60°-(60°-α)=60°+α;
(2)CG=2BD,理由是:
如图,连接BE,过B作BP∥EG,交AC于P,则∠BPC=∠EGP,
∵点D关于直线AB的对称点为点E,
∴∠ABE=∠ABD=60°,
∵∠C=60°,
∴∠EBD+∠C=180°,
∴EB∥GP,
∴四边形EBPG是平行四边形,
∴BE=PG,
∵∠DFG+∠C=120°+60°=180°,
∴∠FGC+∠FDC=180°,
∴∠ADB=∠BGP=∠BPC,
∵AB=BC,∠ABD=∠C=60°,
∴△ABD≌△BCP(AAS),
∴BD=PC=BE=PG,
∴CG=2BD.

练习册系列答案
相关题目