题目内容
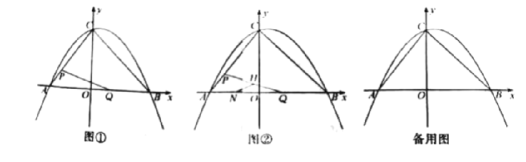
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点A(4,0)和点D(﹣1,0),与y轴交于点C,过点C作BC平行于x轴交抛物线于点B,连接AC
(1)求这个二次函数的表达式;
(2)点M从点O出发以每秒2个单位长度的速度向点A运动;点N从点B同时出发,以每秒1个单位长度的速度向点C运动,其中一个动点到达终点时,另一个动点也随之停动,过点N作NQ垂直于BC交AC于点Q,连结MQ.
①求△AQM的面积S与运动时间t之间的函数关系式,写出自变量的取值范围;当t为何值时,S有最大值,并求出S的最大值;
②是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.
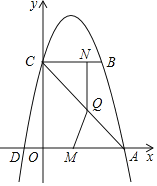
【答案】(1)y=﹣x2+3x+4;(2)①S=-t2+t+2;0≤t≤2;t=![]() 时,S最大值=
时,S最大值=![]() ;②存在,点M的坐标分别为(1,0)和(2,0).
;②存在,点M的坐标分别为(1,0)和(2,0).
【解析】
(1)由待定系数法将AD两点代入即可求解.
(2)①分别用t表示出AM、PQ,由三角形面积公式直接写出含有t的二次函数关系式,由二次函数的最大值可得答案;
②分类讨论直角三角形的直角顶点,然后解出t,求得M坐标.
(1)∵二次函数的图象经过A(4,0)和点D(﹣1,0),
∴![]() ,
,
解得![]() ,
,
所以,二次函数的解析式为y=﹣x2+3x+4.
(2)①延长NQ交x轴于点P,
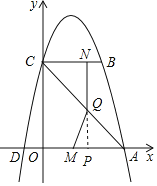
∵BC平行于x轴,C(0,4)
∴B(3,4),NP⊥OA.
根据题意,经过t秒时,NB=t,OM=2t,
则CN=3﹣t,AM=4﹣2t.
∵∠BCA=∠MAQ=45°,
∴QN=CN=3﹣t,
∴PQ=NP﹣NQ=4﹣(1﹣t)=1+t,
∴S△AMQ=![]() AM×PQ=
AM×PQ=![]() (4-2t)(1+t)
(4-2t)(1+t)
=﹣t2+t+2.
∴S=-t2+t+2=-(t-![]() )2+
)2+![]() .
.
∵a=﹣1<0,且0≤t≤2,∴S有最大值.
当t=![]() 时,S最大值=
时,S最大值=![]() .
.
②存在点M,使得△AQM为直角三角形.
设经过t秒时,NB=t,OM=2t,
则CN=3﹣t,AM=4﹣2t,
∴∵∠BCA=∠MAQ=45°.
Ⅰ.若∠AQM=90°,
则PQ是等腰Rt△MQA底边MA上的高.
∴PQ是底边MA的中线,
∴PQ=AP=![]() MA,
MA,
∴1+t=![]() (4﹣2t),
(4﹣2t),
解得,t=![]() ,
,
∴M的坐标为(1,0).
Ⅱ.若∠QMA=90°,此时QM与QP重合.
∴QM=QP=MA,
∴1+t=4﹣2t,
∴t=1,
∴点M的坐标为(2,0).
所以,使得△AQM为直角三角形的点M的坐标分别为(1,0)和(2,0).

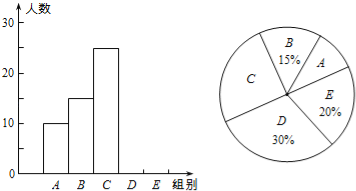
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)若该校共有900名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数.