��Ŀ����
����Ŀ�����κ���y=ax2+bx+c��a��0���Ĵ���ͼ����ͼ��ʾ����������Ϊ����2����9a�������н��ۣ���4a+2b+c��0����5a��b+c=0����������a��x+5����x��1��=��1��������x1��x2����x1��x2����5��x1��x2��1����������|ax2+bx+c|=1���ĸ����������ĸ����ĺ�Ϊ��4��������ȷ�Ľ����У�������
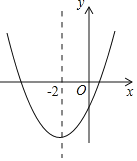
A. 1�� B. 2�� C. 3�� D. 4��
���𰸡�B
�����������������ߵĶ������꣨��2����9a�������ݶ������깫ʽ�����b=4a��c=-5a���Ӷ��ɵ������ߵĽ���ʽΪy=ax2+4ax��5a��Ȼ����ݶ��κ���������һһ�жϼ��ɣ�
��a>0��
�������ߵĶ������꣨��2����9a����
����![]() =��2��
=��2��![]() =��9a��
=��9a��
��b=4a��c=-5a��
�������ߵĽ���ʽΪy=ax2+4ax��5a��
��4a+2b+c=4a+8a��5a=7a��0���ʢ���ȷ��
5a��b+c=5a��4a��5a=��4a��0���ʢڴ���
��������y=ax2+4ax��5a��x���ڣ���5��0������1��0����
��������a��x+5����x��1��=��1��������x1��x2����x1��x2����5��x1��x2��1����ȷ���ʢ���ȷ��
������|ax2+bx+c|=1���ĸ����������ĸ����ĺ�Ϊ��8���ʢܴ���
��ѡB��

 ��Ȥ����¹�֪��ϵ�д�
��Ȥ����¹�֪��ϵ�д� Ӣ��СӢ������Ĭдϵ�д�
Ӣ��СӢ������Ĭдϵ�д� �����ҵ���������ͯ������ϵ�д�
�����ҵ���������ͯ������ϵ�д�