题目内容
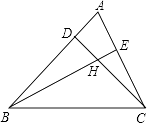
【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
【答案】
(1)解:∵BE⊥AC,∠ACB=70°,
∴∠EBC=90°﹣70°=20°,
∵CD⊥AB,∠ABC=40°,
∴∠DCB=90°﹣40°=50°,
∴∠BHC=180°﹣20°﹣50°=110°.
(2)解:∵BE平分∠ABC,∠ABC=40°,
∴∠EBC=20°,
∵DC平分∠ACB,∠ACB=70°,
∴∠DCB=35°,
∴∠BHC=180°﹣20°﹣35°=125°
【解析】(1)欲求∠BHC,根据∠BHC=180°-∠HBC-∠HCB,只要求出∠HBC,∠HCB即可;
(2)先根据角平分线的定义得到∠EBC=20°,∠DCB=35°,再根据三角形的内角即可求得∠BHC的度数.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
相关题目