题目内容
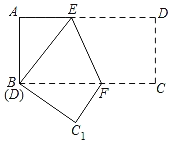
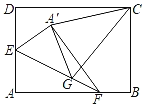
【题目】如图，在矩形纸片ABCD中，AB＝8，BC＝6，点E是AD的中点，点F是AB上一动点．将△AEF沿直线EF折叠，点A落在点A'处．在EF上任取一点G，连接GC，GA'，CA’，则△CGA'的周长的最小值为__．
【答案】7+
【解析】
如图，当点F固定时，连接AC交EF于G，连接A′G，此时△CGA′的周长最小，最小值＝A′G+GC+CA′＝GA+GC+CA′＝AC+CA′．当CA′最小时，△CGA′的周长最小，求出CA′的最小值即可解决问题．
解：如图，当点F固定时，连接AC交EF于G，连接A′G，此时△A′GC的周长最小，最小值＝A′G+GC+CA′＝GA+GC+CA′＝AC+CA′．
∵四边形ABCD是矩形，
∴∠D＝90°，AD＝BC＝6，CD＝AB＝8，
∴AC＝
，
∴△A′CG的周长的最小值＝10+CA′，
当CA′最小时，△CGA′的周长最小，
∵AE＝DE＝EA′＝3，
∴CE＝
，
∵CA′≥EC﹣EA′，
∴CA′≥﹣3，
∴CA′的最小值为﹣3，
∴△CGA′的周长的最小值为7+，
故答案为：7+．
练习册系列答案
相关题目
【题目】某运输公司现将一批152吨的货物运往A，B两地，若用大小货车15辆，则恰好能一次性运完这批货．已知这两种大小货车的载货能力分别为12吨/辆和8吨/辆，其运往A，B两地的运费如下表所示：
目的地(车型) | A地(元/辆) | B地(元/辆) |
大货车 | 800 | 900 |
小货车 | 400 | 600 |
(1)求这15辆车中大小货车各多少辆．(用二元一次方程组解答)
(2)现安排其中的10辆货车前往A地，其余货车前往B地，设前往A地的大货车为x辆，前往A，B两地总费用为w元，试求w与x的函数解析式．
