Question

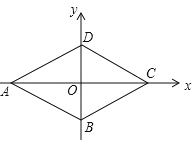
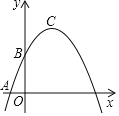
【题目】如图，抛物线（）的顶点为，对称轴与轴交于点，当以为对角线的正方形的另外两个顶点、恰好在抛物线上时，我们把这样的抛物线称为美丽抛物线，正方形为它的内接正方形．

（1）当抛物线是美丽抛物线时，则______；当抛物线是美丽抛物线时，则______；

（2）若抛物线是美丽抛物线时，则请直接写出，的数量关系；

（3）若是美丽抛物线时，（2），的数量关系成立吗？为什么？

（4）系列美丽抛物线（为小于的正整数）顶点在直线上，且它们中恰有两条美丽抛物线内接正方形面积比为．求它们二次项系数之和．

Answer 1

【答案】（1），； （2）；（3）答：成立．见解析；（4）这两条美丽抛物线对应的二次函数的二次项系数和为．

【解析】

（1）分别求出美丽抛物线的顶点A的坐标，根据正方形的性质得到点B的坐标，代入函数解析式求出a或k；

（2）由（1）得到规律；

（3）利用抛物线的平移的性质即可得到答案；

（4）设这两条美丽抛物线的顶点坐标分别为和，（，为小的正整数，且），它们的内接正方形的边长比为，解得，得到这两条美丽抛物线分别为和，根据，，

求出，即可得到答案.

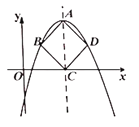
（1）∵抛物线，

∴顶点A的坐标为（0,1），

∴BD=OA=1，

∴点B的坐标为（-0.5,0.5），

将点B的坐标代入，得到0.25a+1=0.5，

解得a=-2，

同理，抛物线是美丽抛物线，

∴顶点A（0，k），

∴B（-， ），

将点B的坐标代入，得，

解得k=-4，

故答案为：，；

（2）由（1）知：

当a=-2时，k=1；当a=时，k=-4，

∴；

（3）答：成立．

∵美丽抛物线沿轴向右或向左平移后得到的抛物线仍然是美丽抛物线．

∴美丽抛物线沿轴经过适当平移后沿到美抛物线．

∴．

（4）设这两条美丽抛物线的顶点坐标分别为和，（，为小的正整数，且），它们的内接正方形的边长比为，

∴，

得．

∴这两条美丽抛物线分别为和．

∵，，

∴，．

∴．

答：这两条美丽抛物线对应的二次函数的二次项系数和为．