Question

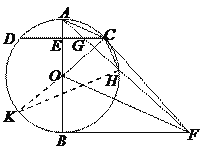
【题目】如图，已知AB是⊙O的直径，C是⊙O上任一点（不与A，B重合），AB⊥CD于E，BF为⊙O的切线，OF∥AC，连接AF，CF，AF与CD交于点G，与⊙O交于点H，连接CH．

（1）求证：CF是⊙O的切线；

（2）求证：EG＝GC；

（3）若cos∠AOC＝，⊙O的半径为9，求CH的长．

Answer 1

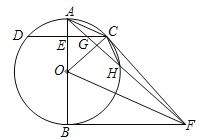
【答案】（1）证明见解析；

（2）证明见解析；

（3）CH的长为

【解析】试题分析：（1）根据OF∥AC，OA=OC，判断出∠BOF=∠COF；然后根据全等三角形判定的方法，判断出△BOF≌△COF，推得∠OCF=∠OBF=90°，再根据点C在⊙O上，即可判断出FC是⊙O的切线． （2）根据已知条件△AEC∽△OBF，根据相似三角形的性质可得 ＝ ，再由∠EAG＝∠BAF，∠AEG＝∠ABF，可得△AEG∽△ABF，即可得 ＝ ，因AB＝2OB，所以 ＝ ，即 ＝ ，所以EC＝2EG，即可得结论EG＝GC ；

（3）延长CO交⊙O于K，连接HK，易证∠CAF＝∠HCF，再由∠AFC＝∠CFH，即可判断△ACF∽△CHF，根据相似三角形的性质可得 ＝ ，因cos∠AOC＝ ，OC＝9，可得 ＝ ＝ ，即可求得OE＝6，所以AE＝3，EC 2＝OC 2－OE 2＝45，由勾股定理可得AC＝ ＝3，再由 ＝ ，可求得BF＝9，再由勾股定理可得AF＝ ＝27，BF、CF都是⊙O的切线，根据切线长定理可得CF＝BF＝9，由此求得CH＝ .

试题解析：

（1）∵BF为⊙O的切线，∴∠OBF＝90°

∵OA＝OC，∴∠OAC＝∠OCA

∵OF∥AC，∴∠OAC＝∠BOF，∠OCA＝∠COF

∴∠BOF＝∠COF

又OB＝OC，OF＝OF，∴△OBF≌△OCF

∴∠OCF＝∠OBF＝90°

∴CF是⊙O的切线

（2）∵AB⊥CD，∴∠AEC＝90°

∴∠AEC＝∠OBF

又∠EAC＝∠BOF，∴△AEC∽△OBF

∴ ＝

∵∠EAG＝∠BAF，∠AEG＝∠ABF

∴△AEG∽△ABF，∴ ＝

∵AB＝2OB，∴ ＝ ，即 ＝

∴EC＝2EG，∴EG＝GC

（3）延长CO交⊙O于K，连接HK

则∠K＝∠CAF，∠K＋∠OCH＝90°

∵∠OCF＝90°，∴∠HCF＋∠OCH＝90°

∴∠CAF＝∠HCF

又∠AFC＝∠CFH，∴△ACF∽△CHF，∴ ＝

∵cos∠AOC＝ ，OC＝9，∴ ＝ ＝

∴OE＝6，∴AE＝3，EC 2＝OC 2－OE 2＝45

∴AC＝ ＝3

∵ ＝ ，∴ ＝ ，∴BF＝9

∴AF＝ ＝27

∵BF、CF都是⊙O的切线，∴CF＝BF＝9

∴ ＝ ，∴CH＝