题目内容
【题目】在△ABC中,∠BAC=90°,AB=AC.
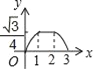
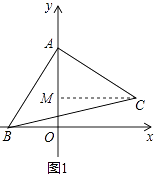
(1)如图1,若A,B两点的坐标分别是A(0,4),B(﹣2,0),求C点的坐标;
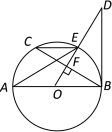
(2)如图2,作∠ABC的角平分线BD,交AC于点D,过C点作CE⊥BD于点E,求证:CE= ![]() BD;
BD;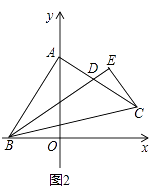
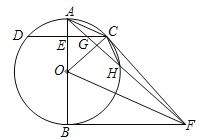
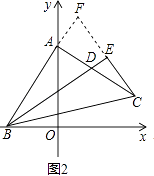
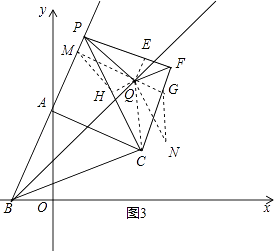
(3)如图3,点P是射线BA上A点右边一动点,以CP为斜边作等腰直角△CPF,其中∠F=90°,点Q为∠FPC与∠PFC的角平分线的交点,当点P运动时,点Q是否恒在射线BD上?若在,请证明;若不在,请说明理由.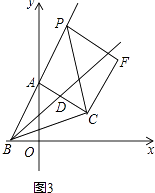
【答案】
(1)
解:如图1中,作CM⊥OA垂足为M,
∵∠AOB=∠BAC=90°,
∴∠BAO+∠CAM=90°,∠BAO+∠ABO=90°,
∴∠ABO=∠CAM,
在△ABO和△CAM中,
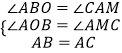 ,
,
∴△ABO≌△CAM,
∴MC=AO=4,AM=BO=2,MO=AO﹣AM=2,
∴点C坐标(4,2)
(2)
证明:如图2,延长CE,BA相交于点F,
∵∠EBF+∠F=90°,∠ACF+∠F=90°,
∴∠EBF=∠ACF,
在△ABD和△ACF中 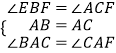 ,
,
∴△ABD≌△ACF(ASA),
∴BD=CF,
在△BCE和△BFE中, 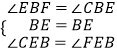 ,
,
∴△BCE≌△BFE(ASA),
∴CE=EF,
∴CE= ![]() BD
BD
(3)
解:结论:点Q恒在射线BD上,
理由如下:
如图3中作QE⊥PF,QG⊥FC,QH⊥PC,QM⊥BP,QN⊥BC,垂足分别为E、G、H、M、N.
在四边形QMBN中,∵∠QMB=∠QNB=90°,
∴∠MQN=180°﹣∠ABC=135°,
同理可证:∠HQG=135°,
∴∠MQN=∠HQG,
∴∠MQH=∠GQN,
∵PQ平分∠FPC,QF平分∠PFC,QE⊥PF,QH⊥PC,QG⊥FC,
∴QE=QH=QG,∠QPH= ![]() ∠CPF=22.5°,
∠CPF=22.5°,
∵∠PMQ=∠PHQ=90°,
∴M、H、Q、P四点共圆,
∴∠HMP=∠HPQ=22.5°,同理∠QNG=22.5°,
∴∠FMQ=∠QNG,
在△MHQ和△NGQ中,
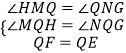 ,
,
∴△MHQ≌△NGQ,
∴QM=QN,
∵QM⊥BP,QN⊥BC,
∴BQ平分∠ABC,
∴点Q恒在射线BD上
【解析】(1)要求点C坐标,作CM⊥AO,只要利用全等三角形的性质求出OM、CM即可;(2)延长CE、BA相交于点F.可以证明Rt△ABD≌Rt△ACF,再证明△BCE≌△BFE得到CE=EF,就可以得出结论;(3)点Q是否恒在射线BD上,只要证明QM=QN,只要证明△M,HQ≌△NGQ即可.
【考点精析】根据题目的已知条件,利用全等三角形的性质的相关知识可以得到问题的答案,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等.

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案