题目内容
 已知:如图,正比例函数y=ax的图象与反比例函数y=
已知:如图,正比例函数y=ax的图象与反比例函数y=| k | x |
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值;
(3)探索:在x轴上是否存在点P,使△OAP是等腰三角形?若存在,请直接写出点P的坐标.
分析:(1)将A坐标代入正比例函数y=ax中求出a的值,确定出正比例解析式,将A坐标代入反比例解析式中求出k的值,确定出反比例解析式;
(2)联立两函数解析式,求出A与B的坐标,在图象上找出反比例函数图象在正比例函数图象上方时x的范围即可;
(3)在x轴上存在点P,使△OAP是等腰三角形,分别为以O为圆心,OA长为半径画弧,与x轴交于P1与P2两点,此时△OAP1与△OAP2都为等腰三角形;作出线段OA的垂直平分线,与x轴交于P3,此时AP3=OP3,△OAP3为等腰三角形,分别求出坐标即可.
(2)联立两函数解析式,求出A与B的坐标,在图象上找出反比例函数图象在正比例函数图象上方时x的范围即可;
(3)在x轴上存在点P,使△OAP是等腰三角形,分别为以O为圆心,OA长为半径画弧,与x轴交于P1与P2两点,此时△OAP1与△OAP2都为等腰三角形;作出线段OA的垂直平分线,与x轴交于P3,此时AP3=OP3,△OAP3为等腰三角形,分别求出坐标即可.
解答: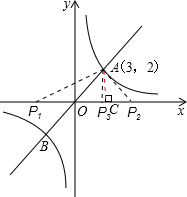 解:(1)将A坐标代入y=ax中,得:2=3a,即a=
解:(1)将A坐标代入y=ax中,得:2=3a,即a=
,
∴正比例函数解析式为y=
x,
将A坐标代入y=
中,得:2=
,即k=6,
∴反比例函数解析式为y=
;
(2)将两函数解析式联立得:
,
解得:
或
,
∴A(3,2),B(-3,-2),
由函数图象得:当x<-3或0<x<3时,反比例函数的值大于正比例函数的值;
(3)在x轴上存在点P,使△OAP是等腰三角形,如图所示:
以O为圆心,OA长为半径画弧,与x轴交于P1与P2两点,此时△OAP1与△OAP2都为等腰三角形,
∵A(3,2),∴OA=
=
,
∴P1(-
,0),
过A作AC⊥x轴,
∵OA=AP2,∴OC=CP2=3,
∴P2(6,0);
作出线段OA的垂直平分线,与x轴交于P3,此时AP3=OP3,△OAP3为等腰三角形,
设AP3=OP3=a,则P3C=OC-OP3=3-a,AC=2,
在Rt△ACP3中,根据勾股定理得:a2=(3-a)2+22,即6a=13,
解得:a=
,
∴P3(
,0),
综上,满足题意的P坐标为(-
,0)或(6,0)或(
,0).
 解:(1)将A坐标代入y=ax中,得:2=3a,即a=
解:(1)将A坐标代入y=ax中,得:2=3a,即a=| 2 |
| 3 |
∴正比例函数解析式为y=
| 2 |
| 3 |
将A坐标代入y=
| k |
| x |
| k |
| 3 |
∴反比例函数解析式为y=
| 6 |
| k |
(2)将两函数解析式联立得:
|
解得:
|
|
∴A(3,2),B(-3,-2),
由函数图象得:当x<-3或0<x<3时,反比例函数的值大于正比例函数的值;
(3)在x轴上存在点P,使△OAP是等腰三角形,如图所示:
以O为圆心,OA长为半径画弧,与x轴交于P1与P2两点,此时△OAP1与△OAP2都为等腰三角形,
∵A(3,2),∴OA=
| 32+22 |
| 13 |
∴P1(-
| 13 |
过A作AC⊥x轴,
∵OA=AP2,∴OC=CP2=3,
∴P2(6,0);
作出线段OA的垂直平分线,与x轴交于P3,此时AP3=OP3,△OAP3为等腰三角形,
设AP3=OP3=a,则P3C=OC-OP3=3-a,AC=2,
在Rt△ACP3中,根据勾股定理得:a2=(3-a)2+22,即6a=13,
解得:a=
| 13 |
| 6 |
∴P3(
| 13 |
| 6 |
综上,满足题意的P坐标为(-
| 13 |
| 13 |
| 6 |
点评:此题考查了反比例函数与一次函数的交点问题,涉及的知识有:等腰三角形的性质,勾股定理,坐标与图形性质,以及待定系数法确定函数解析式,待定系数法是数学中重要的思想方法,学生做题时注意灵活运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知正比例函数y=x与反比例函数y=
如图,已知正比例函数y=x与反比例函数y= 象似双钩,我们称之为“双钩函数”).给出下列几个命题:
象似双钩,我们称之为“双钩函数”).给出下列几个命题: 如图,已知正比例函数y=ax(a≠0)的图象与反比例函致
如图,已知正比例函数y=ax(a≠0)的图象与反比例函致 已知正比例函数y1=x,反比例函数
已知正比例函数y1=x,反比例函数 为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.
为M,又正比例函数y=kx的图象与二次函数相交于两点D、E,且P是线段DE的中点.