题目内容
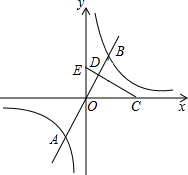 如图,已知正比例函数y=ax(a≠0)的图象与反比例函致y=
如图,已知正比例函数y=ax(a≠0)的图象与反比例函致y=| k | x |
(1)写出反比例函数和正比例函数的解析式;
(2)试计算△COE的面积是△ODE面积的多少倍?
分析:(1)把A的坐标代入反比例函数解析式,即可得到关于k的方程,从而求得k的值.得到反比例函数解析式以及A的坐标,再利用待定系数法即可求得正比例函数解析式;
(2)证明△COE与△ODE相似,求得相似比,根据相似三角形面积的比等于相似比的平方即可求解.
(2)证明△COE与△ODE相似,求得相似比,根据相似三角形面积的比等于相似比的平方即可求解.
解答: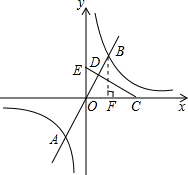 解:(1)由图知k>0,a>0,
解:(1)由图知k>0,a>0,
∵点A(-1,2-k2)在y=
图象上,
∴2-k2=-k,即k2-k-2=0,解得k=2(k=-1舍去),
得反比例函数为y=
.
此时A(-1,-2),代入y=ax,解得a=2,
∴正比例函数为y=2x.
(2)过点B作BF⊥x轴于F.
∵A(-1,-2)与B关于原点对称,
∴B(1,2),即OF=1,BF=2,得OB=
.
由图,易知Rt△OBF∽Rt△OCD,
∴OB:OC=OF:OD,而OD=
=
∴OC=
=2.5.
由Rt△COE∽Rt△ODE,
得
=(
)2=(
×
)2=5.
所以△COE的面积是△ODE面积的5倍.
 解:(1)由图知k>0,a>0,
解:(1)由图知k>0,a>0,∵点A(-1,2-k2)在y=
| k |
| x |
∴2-k2=-k,即k2-k-2=0,解得k=2(k=-1舍去),
得反比例函数为y=
| 2 |
| x |
此时A(-1,-2),代入y=ax,解得a=2,
∴正比例函数为y=2x.
(2)过点B作BF⊥x轴于F.
∵A(-1,-2)与B关于原点对称,
∴B(1,2),即OF=1,BF=2,得OB=
| 5 |
由图,易知Rt△OBF∽Rt△OCD,
∴OB:OC=OF:OD,而OD=
| OB |
| 2 |
| ||
| 2 |
∴OC=
| OB•OD |
| OF |
由Rt△COE∽Rt△ODE,
得
| S△COE |
| S△ODE |
| OC |
| OD |
| 5 |
| 2 |
| 2 | ||
|
所以△COE的面积是△ODE面积的5倍.
点评:本题主要考查了待定系数法求函数解析式,并且运用了相似三角形的性质,相似三角形面积的比等于相似比的平方.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 边形OABD的面积S满足:S1=
边形OABD的面积S满足:S1=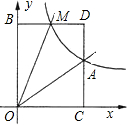 如图,已知正比例函数y=ax与反比例函数y=
如图,已知正比例函数y=ax与反比例函数y=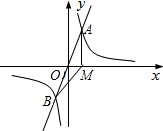 标为1,过点A作x轴的垂线,垂足为M,连接BM.
标为1,过点A作x轴的垂线,垂足为M,连接BM. 如图,已知正比例函数y=kx的图象经过点A(-
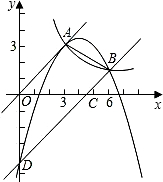
如图,已知正比例函数y=kx的图象经过点A(- 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).