��Ŀ����
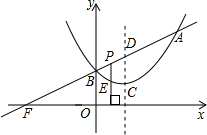
��ͼ����֪���κ���y=ax2+bx+c��ͼ������A��-1��0����B��3��0����C��0��3�������Ķ��� ΪM��������������y=kx��ͼ������κ����ཻ������D��E����P���߶�DE���е㣮
ΪM��������������y=kx��ͼ������κ����ཻ������D��E����P���߶�DE���е㣮
��1����ö��κ����Ľ���ʽ������������M�����ꣻ
��2����֪��E��2��3�����Ҷ��κ����ĺ���ֵ��������������ֵʱ���Ը��ݺ���ͼ����������������Ա���x��ȡֵ��Χ��
��3����kΪ��ֵʱ��0��k��2�����ı���PCMB�����Ϊ
��
���ο���ʽ����֪����D��x1��y1����E��x2��y2�������߶�DE���е�����Ϊ(
��
)��
 ΪM��������������y=kx��ͼ������κ����ཻ������D��E����P���߶�DE���е㣮
ΪM��������������y=kx��ͼ������κ����ཻ������D��E����P���߶�DE���е㣮��1����ö��κ����Ľ���ʽ������������M�����ꣻ
��2����֪��E��2��3�����Ҷ��κ����ĺ���ֵ��������������ֵʱ���Ը��ݺ���ͼ����������������Ա���x��ȡֵ��Χ��
��3����kΪ��ֵʱ��0��k��2�����ı���PCMB�����Ϊ
| 93 |
| 16 |
���ο���ʽ����֪����D��x1��y1����E��x2��y2�������߶�DE���е�����Ϊ(
| x1+x2 |
| 2 |
| y1+y2 |
| 2 |
��������1����֪���κ���y=ax2+bx+c��ͼ������A��-1��0����B��3��0����C��0��3����������κ�������ʽ����ȷ���������ꣻ
��2����E��2��3������y=kx�е���������������ʽ��������������������ʽ�������߽���ʽ���ɵ�D�����꣬����ͼ���������������x�ķ�Χ��
��3����ֱ���������ߵĽ���D��E�����꣬�����е����깫ʽ���P�����꣬���ø����ʾ�ı���PCMB������������ó��ı���PCMB�����Ϊ
ʱ��k��ֵ��
��2����E��2��3������y=kx�е���������������ʽ��������������������ʽ�������߽���ʽ���ɵ�D�����꣬����ͼ���������������x�ķ�Χ��
��3����ֱ���������ߵĽ���D��E�����꣬�����е����깫ʽ���P�����꣬���ø����ʾ�ı���PCMB������������ó��ı���PCMB�����Ϊ
| 93 |
| 16 |
����⣺��1����y=ax2+bx+c����ã�
��
��ã�
��
�ʺ�������ʽΪ��y=-x2+2x+3=-��x-1�� 2+4��
��M��1��4����
��2���ɵ�E��2��3��������������y=kx��ͼ���ϵã�
3=2k��
k=
����y=
x��
��
��
��ã�
��
��D����������-
��-
����
��ͼ���֪�������κ����ĺ���ֵ��������������ʱ���Ա���x��ȡֵ��Χ��-
��x��2��
��3��
��
��ã���D��E����ΪD��
��
•k����
E��
��
•k����
���P����ΪP��
��
•k����0��k��2��֪��P�ڵ�һ���ޣ�
�ɵ�B��3��0����C��0��3����M��1��4����
��S�ı���POMB=
+
��2��4=
��
��S�ı���PCMB=
-S��OPC-S��OPB=
-
��3��
-
��3��
•k��
�����ó���S�ı���PCMB=
��k-
��2+
��
Ҫ��kΪ��ֵʱ��0��k��2���ı���PCMB�����Ϊ
��
�ó�
=
��k-
��2+
��
��0=
��k-
��2��
�ʵ�k=
ʱ���ı���PCMB�����Ϊ
��
|
��ã�
|
�ʺ�������ʽΪ��y=-x2+2x+3=-��x-1�� 2+4��
��M��1��4����
��2���ɵ�E��2��3��������������y=kx��ͼ���ϵã�
3=2k��
k=
| 3 |
| 2 |
| 3 |
| 2 |
��
|
��ã�
|
��D����������-
| 3 |
| 2 |
| 9 |
| 4 |
��ͼ���֪�������κ����ĺ���ֵ��������������ʱ���Ա���x��ȡֵ��Χ��-
| 3 |
| 2 |
��3��
|
��ã���D��E����ΪD��
2-k-
| ||
| 2 |
2-k-
| ||
| 2 |
E��
2-k+
| ||
| 2 |
2-k+
| ||
| 2 |
���P����ΪP��
| 2-k |
| 2 |
| 2-k |
| 2 |
�ɵ�B��3��0����C��0��3����M��1��4����
��S�ı���POMB=
| 1��(3+4) |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
��S�ı���PCMB=
| 15 |
| 2 |
| 15 |
| 2 |
| 1 |
| 2 |
| 2-k |
| 2 |
| 1 |
| 2 |
| 2-k |
| 2 |
�����ó���S�ı���PCMB=
| 3 |
| 4 |
| 1 |
| 2 |
| 93 |
| 16 |
Ҫ��kΪ��ֵʱ��0��k��2���ı���PCMB�����Ϊ
| 93 |
| 16 |
�ó�
| 93 |
| 16 |
| 3 |
| 4 |
| 1 |
| 2 |
| 93 |
| 16 |
��0=
| 3 |
| 4 |
| 1 |
| 2 |
�ʵ�k=
| 1 |
| 2 |
| 93 |
| 16 |
���������⿼���˶��κ�������ʽ�����Լ��ı���������㣬ѧ����������������������ʾ��������ֵ�Ĵ�С��ϵ�����Զ��κ������������ǽ����ص㣮

��ϰ��ϵ�д�
�����Ŀ
 ���������BOF���ƣ������ڣ������P������ꣻ�������ڣ���˵�����ɣ�
���������BOF���ƣ������ڣ������P������ꣻ�������ڣ���˵�����ɣ�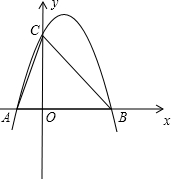
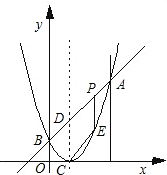 ��ͼ����֪���κ���ͼ��Ķ�������ΪC��1��0����ֱ��y=x+b��ö��κ�����ͼ����A��B���㣬���е�A������Ϊ��3��4������B��y���ϣ���PΪ�߶�AB�ϵ�һ�����㣨��P��A��B���غϣ�������P��x��Ĵ�����ö��κ�����ͼ���ڵ�E��
��ͼ����֪���κ���ͼ��Ķ�������ΪC��1��0����ֱ��y=x+b��ö��κ�����ͼ����A��B���㣬���е�A������Ϊ��3��4������B��y���ϣ���PΪ�߶�AB�ϵ�һ�����㣨��P��A��B���غϣ�������P��x��Ĵ�����ö��κ�����ͼ���ڵ�E��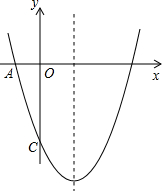 ��ͼ����֪���κ���y=ax2-4x+c��ͼ���������ύ�ڵ�A��-1��0���͵�C��0��-5����
��ͼ����֪���κ���y=ax2-4x+c��ͼ���������ύ�ڵ�A��-1��0���͵�C��0��-5����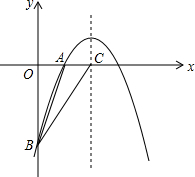 ��2012•��ˮһģ����ͼ����֪���κ���
��2012•��ˮһģ����ͼ����֪���κ���