Question

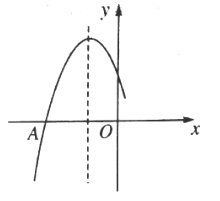
【题目】某商店专门销售某种品牌的玩具，成本为30元/件，每天的销售量y（件）与销售单价x（元）之间存在着如图所示的一次函数关系．

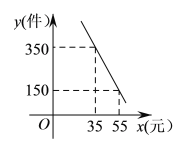
（1）求y与x之间的函数关系式；

（2）当销售单价为多少元时，每天获取的利润最大，最大利润是多少？

（3）为了保证每天的利润不低于3640元，试确定该玩具销售单价的范围．

Answer 1

【答案】（1）；（2）销售单价为50元时，每天获取的利润最大，最大利润是4000元；（3）44≤x≤56

【解析】

（1）直接利用待定系数法求出一次函数解析式即可；

（2）利用w=销量乘以每件利润进而得出关系式求出答案；

（3）利用w=3640，进而解方程，再利用二次函数增减性得出答案．

解：（1）y与x之间的函数关系式为：

把（35，350），（55，150）代入得：

由题意得：

解得：

∴y与x之间的函数关系式为：．

（2）设销售利润为W元

则W=（x﹣30）y=（x﹣30）（﹣10x+700），

W =﹣10x2+1000x﹣21000

W =﹣10（x﹣50）2+4000

∴当销售单价为50元时，每天获取的利润最大，最大利润是4000元．

（3）令W =3640

∴﹣10（x﹣50）2+4000=3640

∴x1=44，x2=56

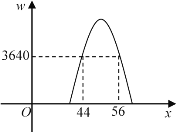
如图所示，由图象得：

当44≤x≤56时，每天利润不低于3640元．