Question

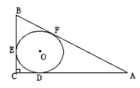
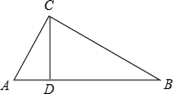
【题目】在Rt△ABC中，CD为斜边AB上的高，AC=3，BC=4，分别用r、r1、r2、表示△ABC，△ACD，△BCD内切圆的半径，则(　　)

A.r+r1+r2=B.r+r1+r2=

C.r﹣r1﹣r2=﹣D.r﹣r1﹣r2=﹣

Answer 1

【答案】A

【解析】

由勾股定理及三角形的面积表示可求出线段CD、AD、BD的长，根据r=，r1=，r2=计算即可.

解：如图，

∵在Rt△ABC中，CD为斜边AB上的高，AC=3，BC=4，

根据勾股定理得AB=5，

，即

CD=

在Rt△ACD 中，由勾股定理得AD=，则BD=．

∵Rt△ABC，Rt△ACD，Rt△BCD的内切圆半径分别是r、r1、r2，

∴r=，r1=，r2=，

∴r+r1+r2=．

故选：A．