Question

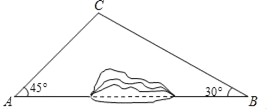
【题目】如图，已知二次函数y＝－x2＋bx＋c与x轴交于A(－2，0)，B两点，对称轴经过点(1，0)．

（1）求b，c的值；

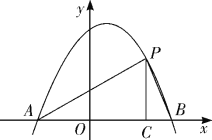
（2）点P是二次函数图象上位于第一象限的一点，过点P作PC⊥x轴，垂足为C，若S△PAC∶S△PBC＝5∶1，求点P的坐标．

Answer 1

【答案】（1）b＝2，c＝8；（2）点P的坐标为(3,5)

【解析】

（1）由二次函数的图象和性质可知，点A、B是二次函数与轴的交点，所以A、B关于对称轴对称，对称轴经过，可知，对称轴为，即可求出点B坐标，把已知点坐标代入二次函数表达式，即可求得b，c的值；

（2）由三角形的面积关系式，两个三角形同高可知，面积比等于底的比，根据AB长度，可求出P点横坐标，代入二次函数表达式，即可求出答案．

解：(1)抛物线的对称轴经过点，

抛物线的对称轴为直线.

点和点在轴上，关于直线对称，

，

抛物线的解析式为，

即，

，

故答案为：，

(2) ，

.

由已知点为二次函数图象上位于第一象限的一点，

点的横坐标为3.

当时，，

点的坐标为，

故答案为：．