题目内容
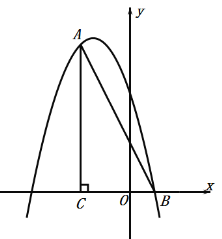
【题目】如图,在平面直角坐标系xOy中,一次函数y=﹣x+2的图象与x轴交于点A与反比例函数![]() (x<0)的图象交于点B,过点B作BC⊥x轴于点C,且OA=OC.
(x<0)的图象交于点B,过点B作BC⊥x轴于点C,且OA=OC.

(1)求点A的坐标和反比例函数的表达式;
(2)若点P是反比例函数![]() (x<0)的图象上的点,过P作PQ∥y轴,交直线AB于点Q,当PQ=BC时,求点P的坐标.
(x<0)的图象上的点,过P作PQ∥y轴,交直线AB于点Q,当PQ=BC时,求点P的坐标.
【答案】(1)A(2,0);![]() ;(2)(3﹣
;(2)(3﹣![]() ,3+
,3+![]() )或(﹣4,2).
)或(﹣4,2).
【解析】
(1)根据一次函数的解析式求得A的坐标,进而B点的横坐标,代入一次函数解析式求得纵坐标,得到B点的坐标,代入![]() 根据待定系数法即可求得反比例函数的解析式;
根据待定系数法即可求得反比例函数的解析式;
(2)设p(a,![]() )(a<0),则Q(a,-a+2),得到PQ=|
)(a<0),则Q(a,-a+2),得到PQ=|![]() -(-a+2)|=|
-(-a+2)|=|![]() +a-2=BC=4|,分两种情况讨论,列出关于a的方程,解方程即可求得.
+a-2=BC=4|,分两种情况讨论,列出关于a的方程,解方程即可求得.
解:(1)在y=﹣x+2中,当y=0时,﹣x+2=0,解得x=2,
∴A(2,0),
又OA=OC,
∴OC=OA=2,
又∵BC⊥x轴于点C,
∴B点的横坐标为﹣2,代入y=﹣x+2,可得B点的纵坐标为4,
∴点B坐标为(﹣2,4),
将点B坐标为(﹣2,4)代入![]() 得,
得,![]() ,
,
∴k=﹣8,
故反比例函数的表达式为![]() ;
;
(2)设P(a,![]() )(a<0),
)(a<0),
∵PQ∥y轴,交直线AB于点Q,
∴Q(a,﹣a+2),
∴PQ=|![]() ﹣(﹣a+2)|=|
﹣(﹣a+2)|=|![]() +a﹣2|,
+a﹣2|,
∵点B坐标为(﹣2,4),
∴BC=4,
当PQ=BC时,有![]() ,当﹣2<a<0时,有
,当﹣2<a<0时,有![]() ,
,
解之得![]() ,舍去正值,
,舍去正值,![]() ,此时点P(3﹣
,此时点P(3﹣![]() ,3+
,3+![]() ),
),
当a<﹣2时,有﹣![]() +a﹣2=﹣4,解之得a1=﹣4,a2=2(舍去),此时点P(﹣4,2),
+a﹣2=﹣4,解之得a1=﹣4,a2=2(舍去),此时点P(﹣4,2),
综上满足条件的点P坐标为(3﹣![]() ,3+
,3+![]() )或(﹣4,2).
)或(﹣4,2).

【题目】据天气预报报道,福建省部分城市某日的最高气温如下表所示:
城市 | 福州 | 厦门 | 宁德 | 莆田 | 泉州 | 漳州 | 龙岩 | 三明 | 南平 |
最高气温(℃) | 11 | 16 | 11 | 13 | 13 | 17 | 16 | 11 | 9 |
则下列说法正确的是( )
A.龙岩的该日最高气温最高B.这组数据的众数是16
C.这组数据的中位数是11D.这组数据的平均数是13