题目内容
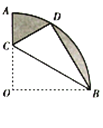
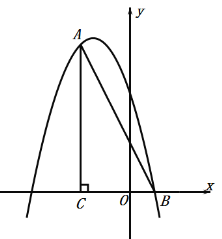
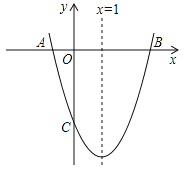
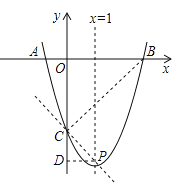
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为x=1,且抛物线经过A(﹣1,0)、C(0,﹣3)两点,与x轴交于另一点B.
(1)求这条抛物线所对应的函数关系式;
(2)在抛物线的对称轴x=1上求一点M,使点M到点A的距离与到点C的距离之和最小,并求出此时点M的坐标;
(3)设点P为抛物线的对称轴x=1上的一动点,求使∠PCB=90°的点P的坐标.
【答案】(1)y=x2-2x-3.(2)M(1,-2).(3 P(1,-4).
【解析】
(1)根据抛物线的对称轴可求出B点的坐标,进而可用待定系数法求出抛物线的解析式;
(2)由于A、B关于抛物线的对称轴直线对称,若连接BC,那么BC与直线x=1的交点即为所求的点M;可先求出直线BC的解析式,联立抛物线对称轴方程即可求得M点的坐标;
(3)若∠PCB=90°,根据△BCO为等腰直角三角形,可推出△CDP为等腰直角三角形,根据线段长度求P点坐标.
(1)∵抛物线的对称轴为x=1,且A(﹣1,0),∴B(3,0);
可设抛物线的解析式为y=a(x+1)(x﹣3),由于抛物线经过C(0,﹣3),则有:a(0+1)(0﹣3)=﹣3,a=1,∴y=(x+1)(x﹣3)=x2﹣2x﹣3;
(2)由于A、B关于抛物线的对称轴直线x=1对称,那么M点为直线BC与x=1的交点;
由于直线BC经过C(0,﹣3),可设其解析式为y=kx﹣3,则有:3k﹣3=0,k=1;
∴直线BC的解析式为y=x﹣3;
当x=1时,y=x﹣3=﹣2,即M(1,﹣2);
(3)设经过C点且与直线BC垂直的直线为直线l,作PD⊥y轴,垂足为D;
∵OB=OC=3,∴CD=DP=1,OD=OC+CD=4,∴P(1,﹣4).

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目