Question

【题目】如图△ABC与△CDE都是等边三角形,且∠EBD=65°,则∠AEB的度数是__________.

Answer 1

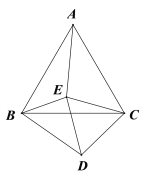
【答案】125°

【解析】

根据等边三角形性质得出AC=BC，CE=CD，∠BAC=60°，∠ACB=∠ECD=60°，求出∠ACE=∠BCD，证△ACE≌△BCD，根据全等三角形的性质得出∠CAE=∠CBD，求出∠ABE+∠BAE=55°，根据三角形内角和定理求出即可．

因为△ABC和△CDE都是等边三角形，

∴AC=BC,CE=CD,∠BAC=60°,∠ACB=∠ECD=60°，

∴∠ACB∠ECB=∠ECD∠ECB，

∴∠ACE=∠BCD，

在△ACE和△BCD中，

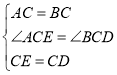
∴△ACE≌△BCD(SAS)，

∴∠CAE=∠CBD，

∵∠EBD=65°，

∴65∠EBC=60°∠BAE，

∴65°(60°∠ABE)=60°∠BAE，

∴∠ABE+∠BAE=55°，

∴∠AEB=180°(∠ABE+∠BAE)=125°.

故答案为：125°