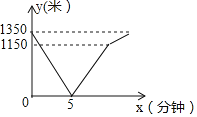ЬтФПФкШн
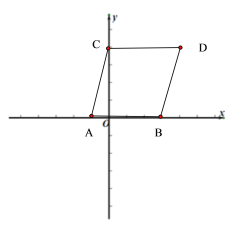
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌAЃЈЃ1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌНЋЯпЖЮABЯШЯђЩЯЦНвЦ![]() ИіЕЅЮЛЃЌдйЯђгвЦНвЦ1ИіЕЅЮЛЃЌЕУЕНЯпЖЮCDЃЌЦфжаЕуAЕФЖдгІЕуЪЧЕуCЃЎСЌНгACЃЌBDЃЌCDЃЎ
ИіЕЅЮЛЃЌдйЯђгвЦНвЦ1ИіЕЅЮЛЃЌЕУЕНЯпЖЮCDЃЌЦфжаЕуAЕФЖдгІЕуЪЧЕуCЃЎСЌНгACЃЌBDЃЌCDЃЎ
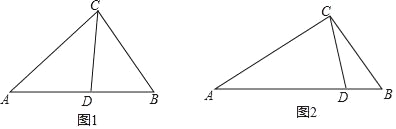
ЃЈ1ЃЉИљОнЬтвтЛГіЭМаЮЃЌжБНгаДГіCЃЌDзјБъЃЛ
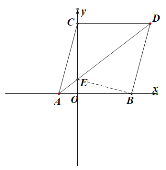
ЃЈ2ЃЉСЌНгADЃЌ ЯпЖЮADгы![]() жсНЛгкЕуEЃЌЧыгУвбОбЇЙ§ЕФжЊЪЖЧѓГіEЕуЕФзјБъЃЈЬсЪОЃКЧызЂвтЫФБпаЮABDCЕФаЮзДЃЉЃЛ
жсНЛгкЕуEЃЌЧыгУвбОбЇЙ§ЕФжЊЪЖЧѓГіEЕуЕФзјБъЃЈЬсЪОЃКЧызЂвтЫФБпаЮABDCЕФаЮзДЃЉЃЛ
ЃЈ3ЃЉP(mЃЌn)ЪЧзјБъЯЕФкШЮвЛЕуЃЌЧв![]() ЃЌСЌНгPCЃЌPDЃЌPOЃЌPBЃЌЕБ
ЃЌСЌНгPCЃЌPDЃЌPOЃЌPBЃЌЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌетбљЕФЕуPДцдкТ№ЃПгаМИИіЃПВЂЧѓГіЕуPЕФзјБъЃЎ
ЪБЃЌетбљЕФЕуPДцдкТ№ЃПгаМИИіЃПВЂЧѓГіЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЭМаЮМћНтЮіЃЌ![]() ЃЛЃЈ2ЃЉЕуEЃЈ0ЃЌ
ЃЛЃЈ2ЃЉЕуEЃЈ0ЃЌ![]() ЃЉЃЛЃЈ3ЃЉетбљЕФPЕужЛгавЛИіЃЌМД
ЃЉЃЛЃЈ3ЃЉетбљЕФPЕужЛгавЛИіЃЌМД![]()
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЦНвЦЕФаджЪЛГіЭМаЮЃЌМДПЩЕУЕНCЃЌDзјБъЃЛ
ЃЈ2ЃЉЯШжЄЫФБпаЮABDCЮЊСтаЮЃЌНсКЯСтаЮЕФаджЪМАЙДЙЩЖЈРэЧѓEЕуЕФзјБъ.
ЃЈ3ЃЉЗжШ§жжЧщПіЬжТлЃКЂйPЕудкЫФБпаЮOBDCФкВП ЂкPдкCDЩЯЗН ЂлPдкABЯТЗН
ЃЈ1ЃЉШчЭМЃЌ![]()
ЃЈ2ЃЉ![]() ЃЌ
ЃЌ
ЁрЫФБпаЮABDCЪЧЦНааЫФБпаЮ
гжгЩЙДЙЩЖЈРэЕУЃК![]()
![]()
ЁрЦНааЫФБпаЮABCDЮЊСтаЮ
СЌНгEBЃЌШчЯТЭМЃКЩш![]()
ЁпдкСтаЮABDCжаЃЌADЪЧBCЕФжаДЙЯпЃЌ
![]()
дкRtЁїOBEжаЃЌгЩЙДЙЩЖЈРэЕУЃК ![]()
НтЕУЃК![]()
ЫљвдЕуEЃЈ0ЃЌ![]() ЃЉ
ЃЉ
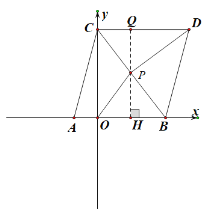
ЃЈ3ЃЉЂйPЕудкЫФБпаЮOBDCФкВПЃЌШчЯТЭМЃК
Й§PЕузїPHЁЭOBгкHЃЌЗДЯђбгГЄPHНЛCDгкQ
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
![]()
![]()
![]() ЃЌ
ЃЌ![]()
![]() ЃЌ
ЃЌ
![]()
![]()
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]()
![]() ЃЌ
ЃЌ
Ёр![]()
ЂкPдкCDЩЯЗНЃЌШчЯТЭМ
Й§PзїPJЁЭOBгкJЃЌгыCDНЛгкKЃЌ
ЭЌЂйРэЕУPKЁЭCD
![]() ЃЌ
ЃЌ![]()
вРЬтвтЕУ![]() НтЕУ
НтЕУ![]()
![]()
![]()
вРЬтвтЕУ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() >3ЃЈЩсЃЉ
>3ЃЈЩсЃЉ

ЂлPдкABЯТЗНЃЌ![]() ЁргыЬѕМўВЛЗћЃЌЩсШЅ
ЁргыЬѕМўВЛЗћЃЌЩсШЅ
злЩЯЫљЪіЃЌетбљЕФPЕужЛгавЛИіЃЌМД![]()

ЁОЬтФПЁПЮЊСЫИјгЮПЭЬсЙЉИќКУЕФЗўЮёЃЌФГОАЧјЫцЛњЖдВПЗжгЮПЭНјааСЫЙигкЁАОАЧјЗўЮёЙЄзїТњвтЖШЁБЕФЕїВщЃЌВЂИљОнЕїВщНсЙћЛцжЦГЩШчЯТВЛЭъећЕФЭГМЦЭМБэ.
ТњвтЖШ | ШЫЪ§ | ЫљеМАйЗжБШ |
ЗЧГЃТњвт | 12 | 10% |
Тњвт | 54 | m |
БШНЯТњвт | n | 40% |
ВЛТњвт | 6 | 5% |

ИљОнЭМБэаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
(1)БОДЮЕїВщЕФзмШЫЪ§ЮЊ______ЃЌБэжаmЕФжЕЮЊ_______ЃЛ
(2)ЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
(3)ОнЭГМЦЃЌИУОАЧјЦНОљУПЬьНгД§гЮПЭдМ3600ШЫЃЌШєНЋЁАЗЧГЃТњвтЁБКЭЁАТњвтЁБзїЮЊгЮПЭЖдОАЧјЗўЮёЙЄзїЕФПЯЖЈЃЌЧыФуЙРМЦИУОАЧјЗўЮёЙЄзїЦНОљУПЬьЕУЕНЖрЩйУћгЮПЭЕФПЯЖЈ.
ЁОЬтФПЁПФГЬдБІЩЬМвМЦЛЎЦНОљУПЬьЯњЪлФГЦЗХЦЖљЭЏЛЌАхГЕ100СОЃЌЕЋгЩгкжжжждвђЃЌЪЕМЪУПЬьЕФЯњЪлСПгыМЦЛЎСПЯрБШгаГіШыЁЃЯТБэЪЧФГжмЕФЯњЪлЧщПіЃЈГЌЖюМЧЮЊе§ЁЂВЛзуМЧЮЊИКЃЉЃК
аЧЦк | вЛ | Жў | Ш§ | ЫФ | Юх | Сљ | Ше |
гыМЦЛЎСПЕФВюжЕ | +4 | -3 | -5 | +14 | -8 | +21 | -6 |
ЃЈ1ЃЉИљОнМЧТМЕФЪ§ОнПЩжЊИУЕъЧАШ§ЬьЙВЯњЪлИУЦЗХЦЖљЭЏЛЌАхГЕ______СОЁЃ
ЃЈ2ЃЉИљОнМЧТМЕФЪ§ОнПЩжЊЯњЪлСПзюЖрЕФвЛЬьБШЯњЪлСПзюЩйЕФвЛЬьЖрЯњЪл______СОЁЃ
ЃЈ3ЃЉИУЕъЪЕааУПШеМЦМўЙЄзЪжЦЃЌУПЯњЪлвЛСОГЕПЩЕУ40дЊЃЌШєГЌЖюЭъГЩШЮЮёЃЌдђГЌЙ§ВПЗжУПСОСэНБ15дЊЃЛЩйЯњЪлвЛСОПл20дЊЃЌФЧУДИУЕъЦЬЕФЯњЪлШЫдБетвЛжмЕФЙЄзЪзмЖюЪЧЖрЩйдЊЃП