题目内容
【题目】如图，□ABCD的对角线AC，BD相交于点O，△OAB是等边三角形，AB＝4，则□ABCD的面积等于________．
【答案】16
【解析】
根据等边三角形性质求出OA=OB=AB，根据平行四边形性质推出AC=BD，根据矩形的判定推出平行四边形ABCD是矩形；求出AC长，根据勾股定理求出BC，根据矩形的面积公式求出即可．
∵△AOB是等边三角形，
∴OA=OB=AB=4，
∵四边形ABCD是平行四边形，
∴AC=2OA，BD=2OB，
∴AC=BD，
∴平行四边形ABCD是矩形.
∵OA=AB=4，AC=2OA=8，四边形ABCD是矩形，
∴∠ABC=90°，
∵在Rt△ABC中,由勾股定理得：BC=
，
∴ABCD的面积是：AB×BC=4×4=16.
练习册系列答案
相关题目
【题目】下列图形都是由同样大小的菱形按照一定规律组成的,请根据排列规律完成下列问题：
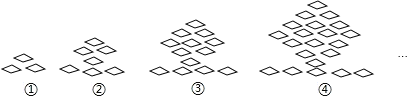
（1）填写下表：
图形序号 | 菱形个数 |
| 3 |
| 7 |
| ______ |
| ______ |
|
|
（2）根据表中规律猜想,图n中菱形的个数
用含n的式子表示,不用说理
；
（3）是否存在一个图形恰好由91个菱形组成？若存在,求出图形的序号；若不存在,说明理由.
