题目内容
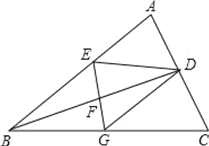
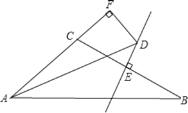
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
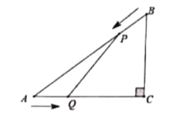
,点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,同时点
匀速运动,同时点![]() 由点
由点![]() 出发沿
出发沿![]() 方向向点
方向向点![]() 匀速运动,它们的速度均为
匀速运动,它们的速度均为![]() .连接
.连接![]() ,设运动时间为
,设运动时间为![]() .
.
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式,并求出当
的函数关系式,并求出当![]() 为何值时,
为何值时,![]() 取得最大值?
取得最大值?![]() 的最大值是多少?
的最大值是多少?
【答案】(1)![]() (2)S=
(2)S=![]() (t
(t![]() )2+
)2+![]() , t=
, t=![]() ,S有最大值,最大值为
,S有最大值,最大值为![]() .
.
【解析】
(1)利用分线段成比例定理构建方程即可解决问题.
(2)构建二次函数,利用二次函数的性质解决问题即可.
(1)∵PQ⊥AC,
∴∠AQP=∠C=90°,
∴PQ∥BC,
∴![]() ,
,
在Rt△ACB中,AB=![]()
∴![]() ,
,
解得t=![]() ,
,
∴t为![]() 时,PQ⊥AC.
时,PQ⊥AC.
(2)如图,作PH⊥AC于H.
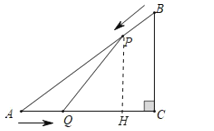
∵PH∥BC,
∴![]() ,
,
∴![]() ,
,
∴PH=![]() (5t),
(5t),
∴S=![]() AQPH=
AQPH=![]() ×t×
×t×![]() (5t)=
(5t)=![]() t2+
t2+![]() t=
t=![]() (t
(t![]() )2+
)2+,
∵![]() <0,
<0,
∴t=![]() ,S有最大值,最大值为
,S有最大值,最大值为![]() .
.

练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | … |
给出以下结论:(1)二次函数y=ax2+bx+c有最小值,最小值为﹣3;(2)当﹣![]() <x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
<x<2时,y<0;(3)已知点A(x1,y1)、B(x2,y2)在函数的图象上,则当﹣1<x1<0,3<x2<4时,y1>y2.上述结论中正确的结论个数为( )
A.0B.1C.2D.3
【题目】某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是()
班级 | 1班 | 2班 | 3班 | 4班 | 5班 | 6班 |
人数 | 52 | 60 | 62 | 54 | 58 | 62 |
A.平均数是58B.中位数是58C.极差是40D.众数是60