题目内容
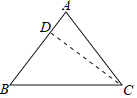
【题目】在△ABC中,∠BAC=90°,AB<AC,M是BC边的中点,MN⊥BC交AC于点N,动点P在线段BA上以每秒![]() cm的速度由点B向点A运动.同时,动点Q在线段AC上由点N向点C运动,且始终保持MQ⊥MP.一个点到终点时两个点同时停止运动,设运动的时间为t秒(t>0).
cm的速度由点B向点A运动.同时,动点Q在线段AC上由点N向点C运动,且始终保持MQ⊥MP.一个点到终点时两个点同时停止运动,设运动的时间为t秒(t>0).
(1)求证:△PBM∽△QNM.
(2)若∠ABC=60°,AB=4![]() cm,
cm,
①求动点Q的运动速度;
②设△APQ的面积为S(cm2),求S与t的等量关系式(不必写出t的取值范围).

【答案】(1)见解析;(2)①Q点的运动速度为1cm/s,②S=﹣![]() t2+8
t2+8![]() .
.
【解析】
(1)由条件可以得出![]() ,
,![]() ,就可以得出
,就可以得出![]() ;
;
(2)①根据直角三角形的性质和中垂线的性质BM、MN的值,再由![]() 就可以求出Q的运动速度;
就可以求出Q的运动速度;
②先由条件表示出AN、AP和AQ,再由三角形的面积公式就可以求出其解析式;
(1)∵MQ⊥MP,MN⊥BC,
∴∠PMN+∠PMB=90°,∠QMN+∠PMN=90°,
∴∠PMB=∠QMN.
∵∠B+∠C=90°,∠C+∠MNQ=90°,
∴∠B=∠MNQ,
∴△PBM∽△QNM.
(2)∵∠BAC=90°,∠ABC=60°,
∴BC=2AB=8![]() cm.AC=12cm,
cm.AC=12cm,
∵MN垂直平分BC,
∴BM=CM=4![]() cm.
cm.
∵∠C=30°,
∴MN=![]() CM=4cm.
CM=4cm.
①设Q点的运动速度为v(cm/s).
∵△PBM∽△QNM.
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴v=1,
答:Q点的运动速度为1cm/s.
②∵AN=AC﹣NC=12﹣8=4cm,
∴AP=4![]() ﹣
﹣![]() t,AQ=4+t,
t,AQ=4+t,
∴S=![]() APAQ=
APAQ=![]() (4
(4![]() ﹣
﹣![]() t)(4+t)=﹣
t)(4+t)=﹣![]() t2+8
t2+8![]() .
.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案
相关题目