题目内容
【题目】如图(1),Rt△ABC中,∠ACB=-90°,CD⊥AB,垂足为D.AF平分∠CAB,交CD于点E,交CB于点F
(1)求证:CE=CF.
(2)将图(1)中的△ADE沿AB向右平移到△A’D’E’的位置,使点E’落在BC边上,其它条件不变,如图(2)所示.试猜想:BE'与CF有怎样的数量关系?请证明你的结论.

【答案】(1)见解析
(2)相等。证明见解析
【解析】
(1)根据平分线的定义可知∠CAF=∠EAD,再根据已知条件以及等量代换即可证明CE=CF,
(2)根据题意作辅助线过点E作EG⊥AC于G,根据平移的性质得出D′E′=DE,再根据已知条件判断出△CEG≌△BE′D′,可知CE=BE′,再根据等量代换可知BE′=CF.
(1)证明:∵AF平分∠CAB,
∴∠CAF=∠EAD,
∵∠ACB=90°,
∴∠CAF+∠CFA=90°,
∵CD⊥AB于D,
∴∠EAD+∠AED=90°,
∴∠CFA=∠AED,又∠AED=∠CEF,
∴∠CFA=∠CEF,
∴CE=CF;
(2)猜想:BE′=CF.
证明:如图,
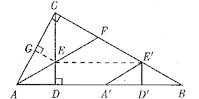
过点E作EG⊥AC于G,连接EE′,
又∵AF平分∠CAB,ED⊥AB,EG⊥AC,
∴ED=EG,
由平移的性质可知:D′E′=DE,
∴D′E′=GE,
∵∠ACB=90°,
∴∠ACD+∠DCB=90°
∵CD⊥AB于D,
∴∠B+∠DCB=90°,
∴∠ACD=∠B,
在△CEG与△BE′D′中,
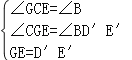 ,
,
∴△CEG≌△BE′D′(AAS),
∴CE=BE′,
由(1)可知CE=CF,
∴BE′=CF.

练习册系列答案
相关题目





