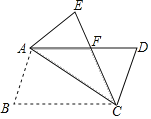
题目内容
【题目】《几何原本》是一部集前人思想和欧几里得个人创造性于一体的不朽之作,它建立了一套从公理、定义出发,论证命题得到定理的几何学论证方法,形成了一个严密的逻辑体系﹣﹣﹣几何学.以下是《几何原本》第一卷中的命题6,请完成它的证明过程.
命题6:如果一个三角形有两个角相等,那么这两个角所对的边也相等.
已知: .
求证: .
证明:若AB≠AC,其中必有一个较大,不妨设AB>AC,在AB上截取BD=AC,
连接DC.
∵ ,
,
,
∴△ACB≌△DBC
∴∠BDC=∠CAB .
又∠BDC>∠CAB .
∴∠BDC与∠CAB即等于又大于,显然是矛盾的.
∴假设不成立,即AB=AC.
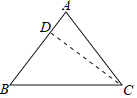
【答案】:△ABC中,∠B=∠C;AB=AC;BD=CA,∠B=∠ACB,BC=CB;(SAS);(全等三角形的对应角相等);(三角形外角性质).
【解析】
运用反证法进行证明,反证法的一般步骤是:①假设命题的结论不成立;②从这个假设出发,经过推理论证,得出矛盾;③由矛盾判定假设不正确,从而肯定原命题的结论正确.
解:已知:△ABC中,∠B=∠C.
求证:AB=AC.
证明:若AB≠AC,其中必有一个较大,不妨设AB>AC,在AB上截取BD=AC,
连接DC.
∵BD=CA,
∠B=∠ACB,
BC=CB,
∴△ACB≌△DBC(SAS)
∴∠BDC=∠CAB(全等三角形的对应角相等).
又∠BDC>∠CAB(三角形外角性质).
∴∠BDC与∠CAB即等于又大于,显然是矛盾的.
∴假设不成立,即AB=AC.
故答案为:△ABC中,∠B=∠C;AB=AC;BD=CA,∠B=∠ACB,BC=CB;(SAS);(全等三角形的对应角相等);(三角形外角性质).

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目