题目内容
【题目】已知:在Rt△ABC中,∠ACB=90°,AB=AC,点D在直线AB上,连接CD,在CD的右侧作CE⊥CD,CD=CE,

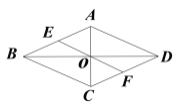
(1)如图1,①点D在AB边上,直接写出线段BE和线段AD的关系;
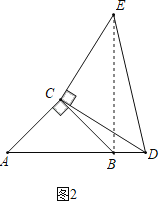
(2)如图2,点D在B右侧,BD=1,BE=5,求CE的长.
(3)拓展延伸
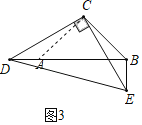
如图3,∠DCE=∠DBE=90,CD=CE,BC=![]() ,BE=1,请直接写出线段EC的长.
,BE=1,请直接写出线段EC的长.
【答案】(1)AD⊥BE;(2)CE=![]() ;(3)CE=
;(3)CE=![]() .
.
【解析】
(1)根据全等三角形的性质得到AD=BE,∠A=∠CBE,求得∠ABE=90°,于是得到结论;
(2)如图2,连接BE,根据全等三角形的性质得到∠A=∠CBE,推出∠DBE=90°,根据勾股定理得到DE=![]() =
=![]() =
=![]() ,即可得到结论;
,即可得到结论;
(3)如图3,过C作CA⊥BC交DB于A,根据已知条件得到D,E,B,C四点共圆,求得∠CDA=∠CEB,根据全等三角形的性质得到AD=BE=1,AC=BC,得到△ACB是等腰直角三角形,于是得到结论.
解:(1)∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE,∠A=∠CBE,
∵∠A+∠ABC=90°,
∴∠ABE=90°,
∴AD⊥BE;
(2)如图2,连接BE,∵∠ACB=∠DCE=90°,
∴∠ACD=∠BCE,
∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴∠A=∠CBE,
∵∠A+∠ABC=90°,
∴∠ABE=90°,
∴∠DBE=90°,
∵BD=1,BE=5,
∴DE=![]() =
=![]() =
=![]() ,
,
∵CD=CE,∠DCE=90°,
∴CE=![]() DE=
DE=![]() ;
;
(3)如图3,过C作CA⊥BC交DB于A,
∵∠DCE=90°,
∴∠DCA=∠ECB,
∵∠DCE=∠DBE=90°,
∴D,E,B,C四点共圆,
∴∠CDA=∠CEB,
∵CD=CE,
∴△CDA≌△CEB(ASA),
∴AD=BE=1,AC=BC,
∴△ACB是等腰直角三角形,
∴AB=![]() BC=2,
BC=2,
∴BD=3,
∴DE=![]() =
=![]() =
=![]() ,
,
∴CE=![]() DE=
DE=![]() .
.

 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案