题目内容
【题目】在平面直角坐标系xOy中，抛物线 
经过点A（0，2）和B（1， 
）．
（1）求该抛物线的表达式；
（2）已知点C与点A关于此抛物线的对称轴对称，点D在抛物线上，且点D的横坐标为4，求点C与点D的坐标；
（3）在（2）的条件下，将抛物线在点A，D之间的部分（含点A，D）记为图象G，如果图象G向下平移t（t＞0）个单位后与直线BC只有一个公共点，求t的取值范围．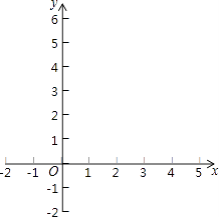
【答案】
（1）解：把A（0，2）和B（1， 
）代入 
得 
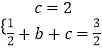，解得 
，
所以抛物线解析式为y= 
x2﹣x+2
（2）解：∵y= x2﹣x+2= （x﹣1）2+ ，
∴抛物线的对称轴为直线x=1，
∵点C与点A关于此抛物线的对称轴对称，
∴C点坐标为（2，2）；
当x=4时，y= x2﹣x+2=8﹣4+2=6，
∴D点坐标为（4，6）
（3）解：如图，
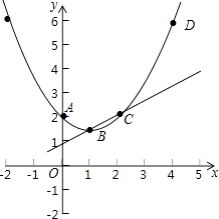
设直线BC的解析式为y=mx+n，
把B（1， ），C（2，2）代入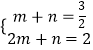得 
，解得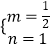 
，
∴直线BC的解析式为y= x+1，
当x=0时，y= x+1=1，
∴点图象G向下平移1个单位时，点A在直线BC上，
当x=4时，y= x+1=3，
∴点图象G向下平移3个单位时，点D在直线BC上，
∴当1＜t≤3时，图象G向下平移t（t＞0）个单位后与直线BC只有一个公共点．
【解析】（1）利用待定系数法可求出二次函数的解析式；
（2）把二次函数的解析式化成顶点式，再利用抛物线的对称性可求出点C的坐标；把x=4代入二次函数的解析式可求出纵坐标；
（3）利用待定系数法可求出直线BC的解析式，由x=0、x=4分别求出y的值，从而可知点A、D在直线BC上，进而可得t的取值范围.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小．
