Question

【题目】如图，在数学实践课中，小明为了测量学校旗杆CD的高度，在地面A处放置高度为1．5米的测角仪AB，测得旗杆顶端D的仰角为32°，AC为22米，求旗杆CD的高度．（结果精确到0．1米．参考数据：sin32°= 0．53，cos32°= 0．85，tan32°= 0．62）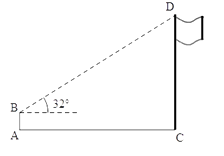

Answer 1

【答案】简介：由题意得AC=22米，AB=1．5米，

过点B做BE⊥CD，交CD于点E，

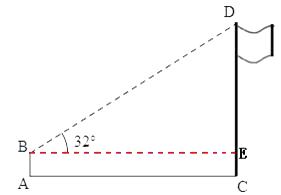
∵∠DBE=32°，

∴DE=BEtan32°≈22×0．62=13．64米，

∴CD=DE+CE=DE+AB=13．64+1．5≈15．1米．

答：旗杆CD的高度约15．1米．

【解析】过点B做BE⊥CD，交CD于点E，在Rt△BDE中，由tan∠DBE=，可求出DE的长，再由CD=DE+CE=DE+AB可求出CD的长.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点，需要掌握仰角：视线在水平线上方的角；俯角：视线在水平线下方的角才能正确解答此题．